1. Στερεό σώμα στρέφεται γύρω από σταθερό άξονα περιστροφής. Η γραφική παράσταση της γωνιακής ταχύτητας του στερεού με το χρόνο φαίνεται στο παρακάτω διάγραμμα.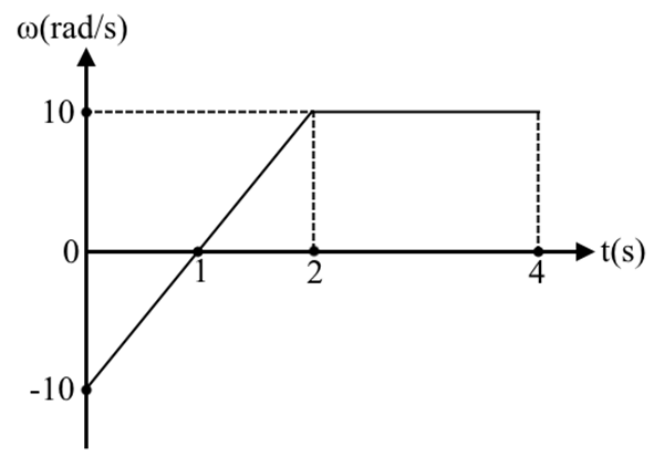
Α) Η γωνιακή μετατόπιση του στερεού απ’ τη στιγμή \[t=0\] ως τη στιγμή \[t=4\, s\] είναι ίση με: α) \[20\, rad\], β) \[30\, rad\], γ) \[40\, rad\].
Β) Ο αριθμός των περιστροφών που διαγράφει ο τροχός ανεξαρτήτως φοράς κίνησης είναι:
α) \[\frac{10}{π}\], β) \[\frac{15}{π}\], γ) \[\frac{20}{π}\].
2. Στερεό σώμα εκτελεί στροφική κίνηση γύρω από σταθερό άξονα με σταθερή γωνιακή επιτάχυνση. Δύο σημεία Β και Γ έχουν επιτρόχιες επιταχύνσεις μέτρων \[α_{επ_Β}\] και \[α_{επ_Γ}\] αντίστοιχα και ισχύει \[α_{επ_Γ}=2α_{επ_Β }\].Α) Οι κεντρομόλες επιταχύνσεις των δύο αυτών σημείων την ίδια στιγμή \[t_1\] έχουν μέτρα \[α_{κ_{Γ_1 }}\] και \[α_{κ_{Β_1 }}\] αντίστοιχα και ισχύει:
α) \[ \frac{ α_{κ_{Γ_1 }} } {α_{κ_{Β_1 }} } =\frac{1}{2} \],
β) \[ \frac{ α_{κ_{Γ_1 }} }{ α_{κ_{Β_1 }} } =2\],
γ) \[ \frac{ α_{κ_{Γ_1 }} }{α_{κ_{Β_1 }} } =\frac{1}{4} \],
δ) \[ \frac{ α_{κ_{Γ_1 }} }{ α_{κ_{Β_1 }} } =4\].
Β) Τα μέτρα των επιταχύνσεων \[α_Β,\, α_Γ\] των σημείων Β, Γ αντίστοιχα έχουν λόγο \[\frac{α_Β}{α_Γ}\] ίσο με:
α) \[\frac{1}{2}\], β) \[2\], γ) \[\sqrt{2}\], δ) \[\frac{\sqrt{2} } {2}\].
4. Στερεό σώμα στρέφεται γύρω από σταθερό άξονα περιστροφής εκτελώντας ομαλά μεταβαλλόμενη κίνηση. Για την κυκλική κίνηση ενός κινούμενου σημείου του στερεού σώματος, ποιες από τις παρακάτω προτάσεις είναι σωστές; 7. Ο τροχός του παρακάτω σχήματος στρέφεται γύρω από οριζόντιο άξονα \[x' x\] που είναι κάθετος στη βάση του και περνά απ’ τα κέντρα τους. Ο τροχός στρέφεται κατά τη φορά των δεικτών του ρολογιού με σταθερή γωνιακή ταχύτητα. Ποιες από τις ακόλουθες προτάσεις είναι σωστές;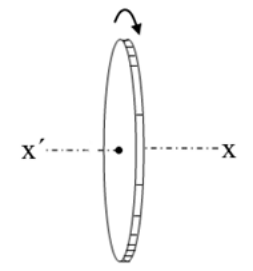
9. Τροχός στρέφεται γύρω από σταθερό άξονα περιστροφής που είναι κάθετος στις βάσεις του και η γωνιακή του ταχύτητα μεταβάλλεται με σταθερό ρυθμό. Ποιες από τις παρακάτω προτάσεις είναι σωστές; Η \[\vec{α}_{γων}\] του τροχού: 10. Δίσκος στρέφεται γύρω από σταθερό άξονα που διέρχεται απ’ το κέντρο του και είναι κάθετος στο επίπεδό του. Δύο σημεία του δίσκου Β, Γ απέχουν απ’ τον άξονα περιστροφής του αποστάσεις \[r_B,\, r_Γ\] με \[r_Γ=3r_B\].Α. Αν σε χρόνο \[Δt\] η επιβατική ακτίνα του Β διαγράψει γωνία \[Δθ_Β\], η επιβατική ακτίνα του Γ στον ίδιο χρόνο θα διαγράψει γωνία \[Δθ_Γ\] για την οποία ισχύει:
α) \[Δθ_Β=Δθ_Γ\], β) \[Δθ_Β=\frac{Δθ_Γ}{3} \], γ) \[ Δθ_Β=3Δθ_Γ\].
Β. Αν σε χρόνο \[Δt\] το σημείο Β διανύσει μήκος τόξου \[Δs_B\] το σημείο Γ στον ίδιο χρόνο θα διανύσει τόξο \[Δs_Γ\] για το οποίο ισχύει:
α) \[Δs_Γ=Δs_B\], β) \[Δs_Γ=3Δs_B\], γ) \[Δs_Γ=\frac{Δs_B}{3}\].
Γ) Για τα μέτρα \[α_{κ_Β},\, α_{κ_Γ }\] των κεντρομόλων επιταχύνσεων την ίδια στιγμή ισχύει:
α) \[ α_{κ_Β }=\frac{ α_{κ_Γ} } {3} \],
β) \[ α_{κ_Β }=3α_{κ_Γ } \],
γ) \[ α_{κ_Β }=α_{κ_Γ } \],
δ) \[ α_{κ_Β }=α_{κ_Γ }=0\], αν η κίνηση του δίσκου είναι ομαλή στροφική.
11. Ποιες από τις παρακάτω προτάσεις είναι σωστές; Στερεό σώμα είναι: 15. Ομογενής ράβδος στρέφεται γύρω από σταθερό άξονα περιστροφής. Η γωνιακή ταχύτητα της ράβδου μεταβάλλεται με το χρόνο σύμφωνα με το παρακάτω διάγραμμα.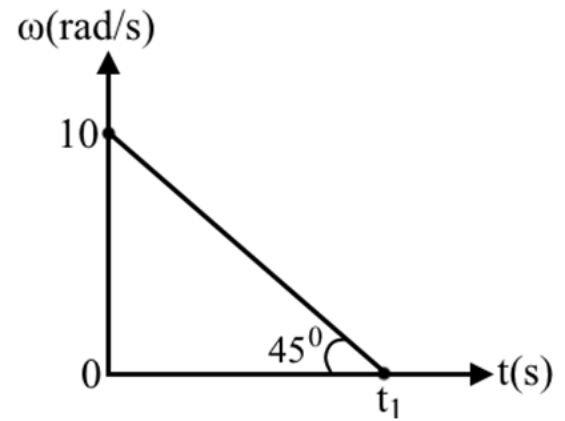
Α) Η ράβδος ακινητοποιείται τη χρονική στιγμή \[t_1\] που είναι ίση με:
α) \[1\, s\], β) \[\sqrt{3}\, s\], γ) \[10\, s\].
Β) Η γωνιακή μετατόπιση της ράβδου απ’ τη στιγμή \[t=0\] ως τη στιγμή \[t_1\] είναι:
α) \[5\, rad\], β) \[50\, rad\], γ) \[100\, rad\].
16. Ένας δίσκος εκτελεί στροφική κίνηση γύρω από σταθερό άξονα περιστροφής ο οποίος διέρχεται από κάποιο σημείο του και είναι κάθετος στο επίπεδο του. Αν η γωνιακή ταχύτητα του σώματος είναι σταθερή, τότε: 17. Στερεό σώμα εκτελεί στροφική μεταβαλλόμενη κίνηση γύρω από σταθερό άξονα περιστροφής. Ποια απ’ τις παρακάτω προτάσεις είναι σωστή; Όλα τα σημεία του στερεού που κινούνται την ίδια χρονική στιγμή: 18. Ομογενής συμπαγής σφαίρα στρέφεται γύρω από σταθερό άξονα που ταυτίζεται με τη διεύθυνση μιας διαμέτρου της. Η γωνιακή ταχύτητα της σφαίρας μεταβάλλεται με το χρόνο σύμφωνα με το παρακάτω διάγραμμα.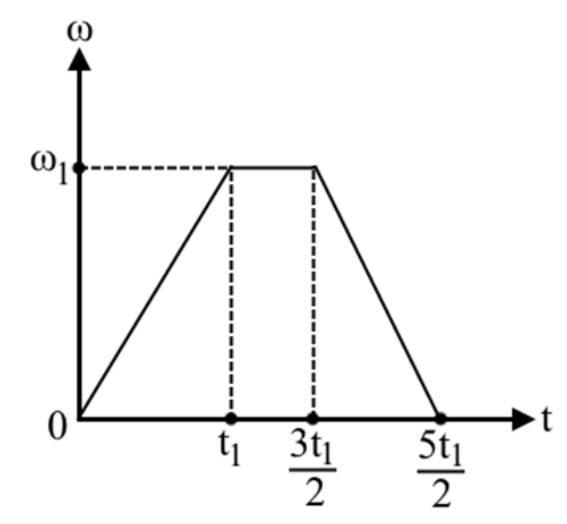
Α) Αν \[Δθ_1,\, Δθ_2,\, Δθ_3\] οι γωνιακές μετατοπίσεις της σφαίρας τις χρονικές διάρκειες από \[0\] ως \[t_1\], από \[t_1\] ως \[\frac{3t_1}{2}\] και από \[\frac{3t_1}{2}\] ως \[\frac{5t_1}{2}\] αντίστοιχα ισχύει: α) \[Δθ_1=Δθ_2=Δθ_3\], β) \[Δθ_1=Δθ_2=-Δθ_3\],
γ) \[Δθ_2=2Δθ_1=2Δθ_3\], δ) \[Δθ_2=2Δθ_1=-2Δθ_3\].
Β) Η φορά της στροφικής κίνησης:
α) αλλάζει τη στιγμή \[t_1\],
β) αλλάζει τη στιγμή \[\frac{3t_1}{2}\],
γ) δεν αλλάζει ποτέ.
19. Η ράβδος ΟΑ μήκους \[\ell\] του παρακάτω σχήματος στρέφεται γύρω από σταθερό κατακόρυφο άξονα που διέρχεται απ’ το άκρο της Ο. Η στροφική κίνηση της ράβδου είναι ομαλά επιβραδυνόμενη και έχει φορά αντίθετη των δεικτών του ρολογιού.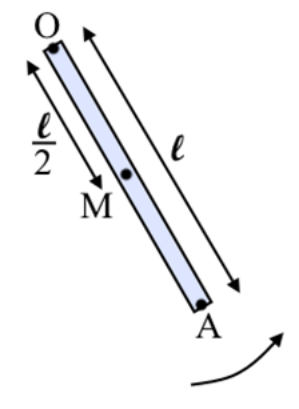
Α. Για τα μέτρα των γραμμικών ταχυτήτων \[υ_Μ, \, υ_Α\] των σημείων Μ, Α την ίδια στιγμή ισχύει:
α) \[υ_Μ=υ_Α\], β) \[υ_Μ=2υ_Α\], γ) \[υ_Α=2υ_Μ\].
Β. Για τα μέτρα των κεντρομόλων επιταχύνσεων \[α_κ\] των σημείων Μ, Α την ίδια στιγμή ισχύει:
α) \[α_{κ_Μ }=α_{κ_Α }\], β) \[α_{κ_Α }=2α_{κ_Μ }\], γ) \[α_{κ_Α }=4α_{κ_Μ }\].
20. Ζεύγος δυνάμεων ονομάζεται το σύστημα: 21. Δίσκος εκτελεί στροφική κίνηση γύρω από σταθερό κατακόρυφο άξονα που είναι κάθετος στις βάσεις του και διέρχεται απ’ τα κέντρα τους. Η γωνία που διαγράφει ο δίσκος με το χρόνο δίνεται απ’ τη σχέση \[θ=10t\] (S.I.). Ποιες από τις παρακάτω προτάσεις είναι σωστές; 22. Ποιες από τις παρακάτω προτάσεις είναι σωστές; Η γωνιακή ταχύτητα ενός στερεού σώματος που εκτελεί στροφική κίνηση γύρω από σταθερό άξονα περιστροφής: 24. Η ράβδος ΟΑ του παρακάτω σχήματος στρέφεται γύρω από σταθερό κατακόρυφο άξονα κάθετο στη διεύθυνσή της που διέρχεται απ’ το άκρο της Ο με τη φορά που φαίνεται στο σχήμα.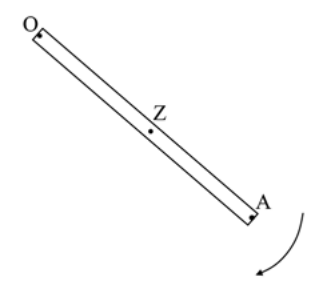
25. Τροχός στρέφεται γύρω από σταθερό άξονα περιστροφής που είναι κάθετος στις βάσεις του και διέρχεται απ’ τα κέντρα τους με σταθερή γωνιακή ταχύτητα. Ποιες από τις παρακάτω προτάσεις είναι σωστές; 29. Ποιες από τις παρακάτω προτάσεις είναι σωστές; Στην μεταφορική κίνηση ενός στερεού σώματος: 30. Να επιλέξετε τις σωστές απαντήσεις. Η ροπή ενός ζεύγους δυνάμεων τετραπλασιάζεται όταν 