1. Το παρακάτω στερεό (σχ. α) είναι ένα καρούλι. Αυτό αποτελείται από έναν ομογενή κύλινδρο που στα άκρα του έχουμε κολλήσει δύο όμοιους ομογενείς δίσκους έτσι ώστε τα κέντρα τους να βρίσκονται πάνω στον άξονα του κυλίνδρου. Η ακτίνα του κυλίνδρου είναι \[r\] ενώ του κάθε δίσκου είναι \[R\]. Τοποθετώ το καρούλι πάνω στις δοκούς έτσι ώστε οι περιφέρειες των δίσκων ν’ ακουμπούν σ’ αυτές, ενώ ο κύλινδρος να στηρίζεται μόνο στους δίσκους χωρίς να έρχεται σε επαφή με το έδαφος ή τις δοκούς. Το καρούλι αρχίζει να κινείται και το κέντρο μάζας του έχει σταθερή ταχύτητα μέτρου \[υ_{cm}\] και το καρούλι στρέφεται με γωνιακή ταχύτητα μέτρου \[ω\] (σχ. β).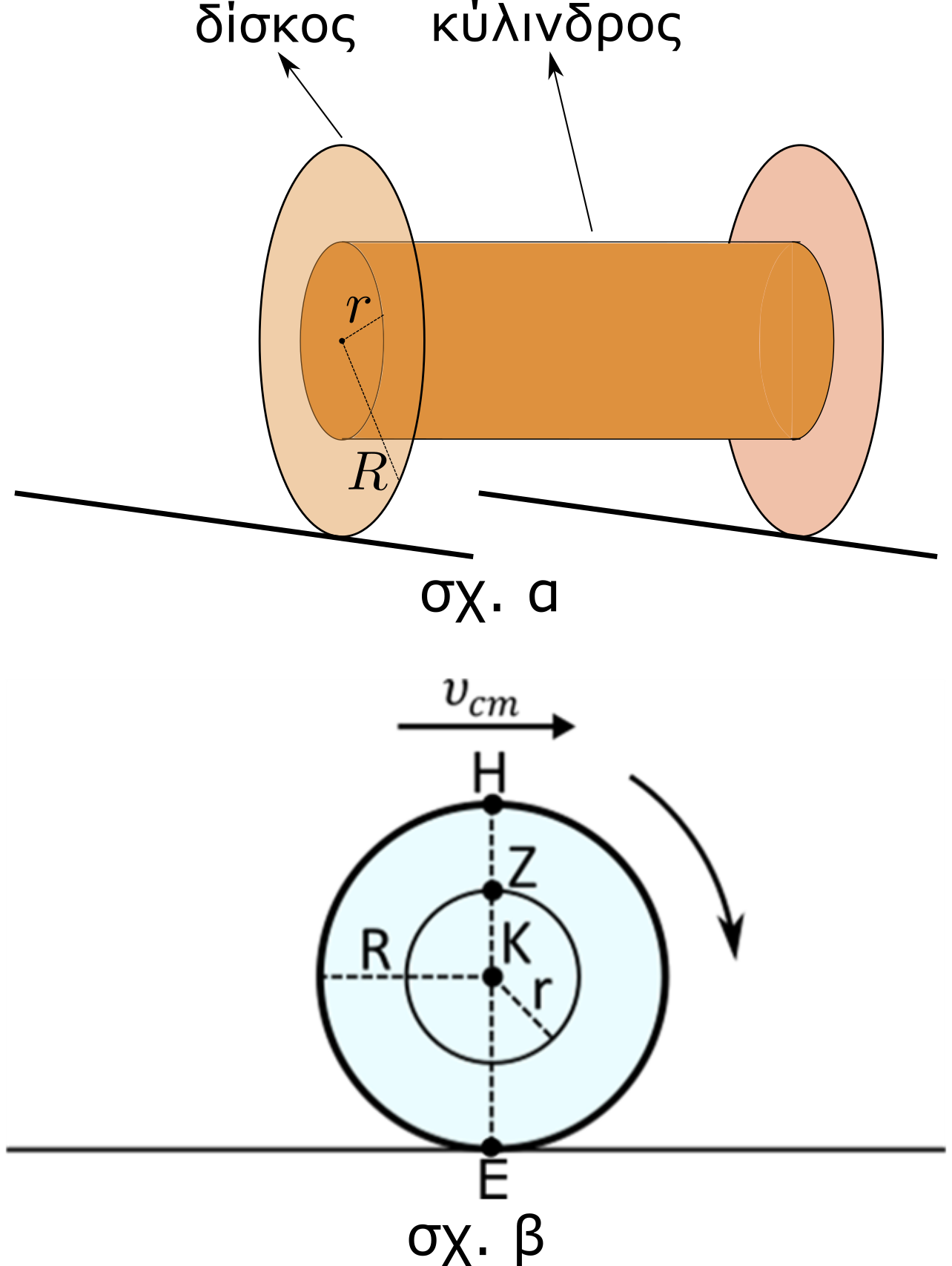
A) Το μέτρο της ταχύτητας του κέντρου μάζας του τροχού είναι:
α) \[ ωR\], β) \[ωr\], γ) \[ω(R-r)\].
Β) Το ανώτερο σημείο Ζ της περιφέρειας του κυλίνδρου έχει ταχύτητα μέτρου:
α) \[2υ_{cm}\], β) \[υ_{cm} \left( \frac{r}{R}+1 \right)\], γ) \[υ_{cm} \left( \frac{R}{r}-1 \right)\].
Γ) Το ανώτερο σημείο Η της περιφέρειας του ενός δίσκου έχει ταχύτητα μέτρου:
α) \[2υ_{cm}\], β) \[ω\left( \frac{R}{r}+1 \right)\], γ) \[ ω \left( \frac{R}{r}-1\right) \].
Δ) Το σημείο Ε της περιφέρειας του ενός δίσκου που βρίσκεται σε επαφή με το έδαφος έχει επιτάχυνση μέτρου:
α) \[0\], β) \[ω^2 R\], γ) \[ω^2 r\].
10. Το στερεό σώμα του παρακάτω σχήματος α στρέφεται γύρω από τον σταθερό άξονα \[z' z\] αντίρροπα των δεικτών του ρολογιού. Η γωνιακή ταχύτητα μεταβάλλεται με το χρόνο σύμφωνα με το παρακάτω διάγραμμα. Ποιες από τις παρακάτω προτάσεις είναι σωστές;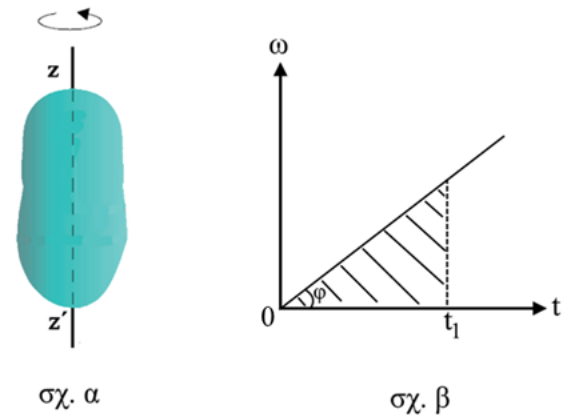
12. Ο ομογενής τροχός ακτίνας \[R\] του παρακάτω σχήματος αρχίζει να κυλίεται χωρίς να ολισθαίνει την \[t=0\] σε οριζόντιο έδαφος και η επιτάχυνση του κέντρου μάζας του είναι σταθερή. Μια χρονική στιγμή \[t_1\] η γωνιακή ταχύτητα του τροχού έχει μέτρο \[ω_1\] και η ταχύτητα του κέντρου μάζας του τροχού έχει μέτρο \[υ_{1_{cm}}\] και έχει τη φορά που φαίνεται στο σχήμα. Τα σημεία Γ και Δ είναι τα άκρα της οριζόντιας διαμέτρου του τροχού. Ποιες απ’ τις επόμενες προτάσεις είναι σωστές;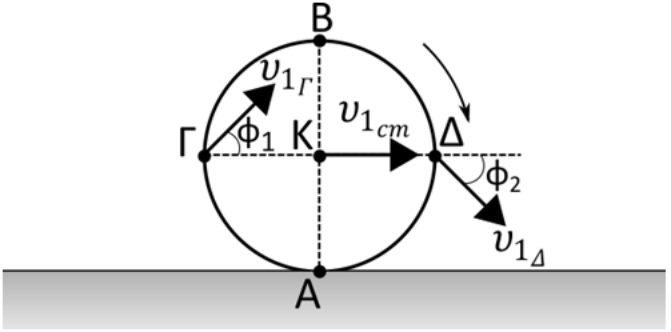
17. Ομογενής τροχός κυλίεται χωρίς να ολισθαίνει και η μεταφορική του κίνηση είναι ομαλά επιταχυνόμενη. Ποια απ’ τις επόμενες προτάσεις είναι σωστή; 18. Στερεό σώμα εκτελεί στροφική κίνηση και η γωνιακή του ταχύτητα δίνεται απ’ τη σχέση \[ω=5+2t\] (S.I.). Ποιες από τις παρακάτω προτάσεις είναι σωστές; 19. Ο τροχός του παρακάτω σχήματος εκτελεί στροφική κίνηση γύρω από σταθερό κατακόρυφο άξονα \[z' z\] που είναι κάθετος στη βάση του με τη φορά που φαίνεται στο σχήμα. Το μέτρο της γωνιακής του ταχύτητας μειώνεται με το χρόνο. Ποιες απ’ τις παρακάτω προτάσεις είναι σωστές;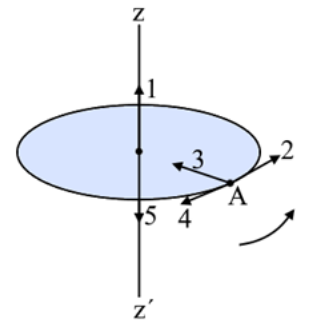
20. Ομογενής τροχός κυλίεται χωρίς να ολισθαίνει με σταθερή επιτάχυνση μέτρου \[α_{cm}\] στην μεταφορική του κίνηση και σταθερή γωνιακή επιτάχυνση μέτρου \[α_{γων}\]. Τη στιγμή \[t_1\] το κέντρο μάζας του τροχού έχει μέτρο \[υ_{1_{cm}}\] και η γωνιακή ταχύτητα του τροχού έχει μέτρο \[ω_1\]. Ποιες από τις ακόλουθες προτάσεις είναι σωστές;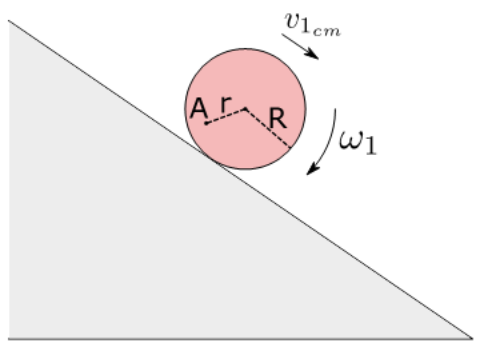
21. Στον ομογενή δίσκο ακτίνας \[R\] του παρακάτω σχήματος έχουμε δημιουργήσει αυλάκι με κέντρο το κέντρο του δίσκου και ακτίνας \[r=\frac{R}{2}\]. Στην περιφέρεια που δημιουργεί το αυλάκι τυλίγουμε πολλές φορές λεπτό και μη εκτατό νήμα. Στο ελεύθερο άκρο Α του νήματος ασκώ σταθερή δύναμη \[F\] και ο κύλινδρος αρχίζει να κυλίεται χωρίς να ολισθαίνει ενώ το νήμα ξετυλίγεται χωρίς να ολισθαίνει στο αυλάκι. Αν μέχρι τη στιγμή \[t_1\] το νήμα έχει ξετυλιχθεί κατά \[\ell\]: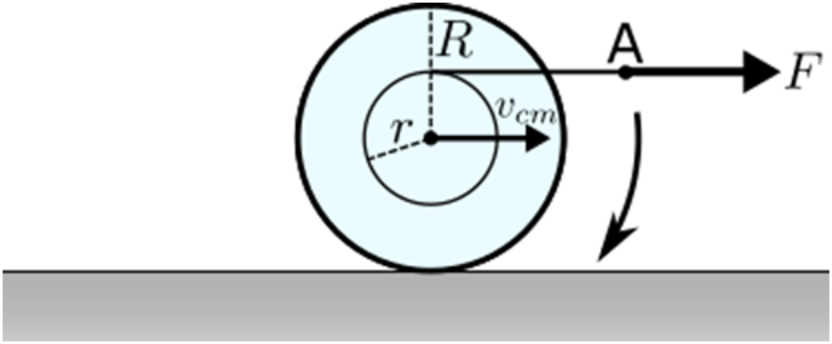
Α) Aν το κέντρο μάζας τη στιγμή \[t_1\] έχει ταχύτητα μέτρου \[υ_{cm}\], το άκρο Α έχει ταχύτητα μέτρου:
α) \[\frac{3}{2} υ_{cm} \], β) \[2υ_{cm}\], γ) \[υ_{cm}\].
Β) Αν το κέντρο μάζας του δίσκου έχει επιτάχυνση μέτρου \[α_{cm}\], τότε το ελεύθερο άκρο Α του νήματος έχει επιτάχυνση μέτρου:
α) \[α_{cm}\], β) \[\frac{3}{2} α_{cm}\], γ) \[2α_{cm}\].
22. Η ομογενής ράβδος ΟΑ του παρακάτω σχήματος στρέφεται πάνω σε οριζόντιο επίπεδο γύρω από σταθερό κατακόρυφο άξονα. Στο σχήμα φαίνονται οι κατευθύνσεις της γωνιακής επιτάχυνσης της ράβδου και της επιτρόχιας επιτάχυνσης του άκρου της Α. Ποια απ’ τις επόμενες προτάσεις είναι σωστή;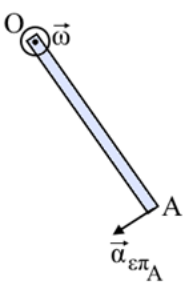
23. Στερεό εκτελεί στροφική κίνηση γύρω από σταθερό άξονα περιστροφής. Στο παρακάτω διάγραμμα φαίνεται η γραφική παράσταση της γωνιακής ταχύτητας του στερεού με το χρόνο. Ποιες από τις παρακάτω προτάσεις είναι σωστές;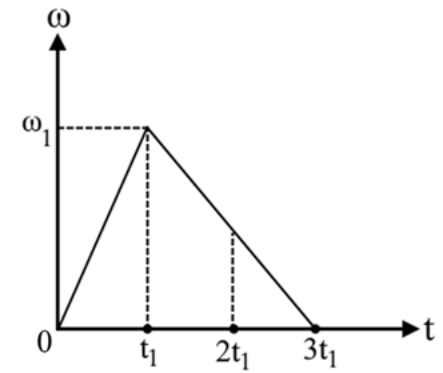
28. Ομογενής τροχός ακτίνας \[R\] κυλίεται χωρίς να ολισθαίνει πάνω σε οριζόντιο επίπεδο και η γωνιακή του ταχύτητα είναι σταθερή και έχει μέτρο \[ω\]. Ποιες από τις επόμενες προτάσεις είναι σωστές; 30. Στο παρακάτω σχήμα ο ομογενής δίσκος ακτίνας \[R\] κυλίεται χωρίς να ολισθαίνει, ενώ στο ανώτερο άκρο της περιφέρειάς του έχουμε ακουμπήσει λεπτή σανίδα που μεταφέρεται με κατάλληλο μηχανισμό ώστε να μην ολισθαίνει πάνω στο δίσκο και να μένει συνεχώς οριζόντια.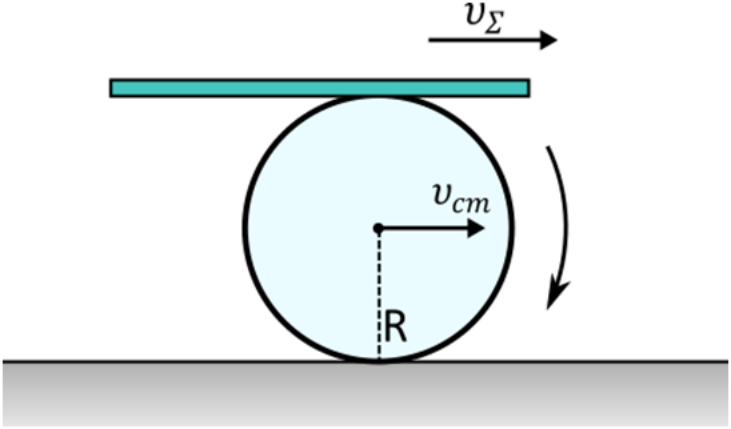
Α) Αν τη στιγμή \[t_1\] ο τροχός έχει γωνιακή ταχύτητα μέτρου \[ω\], την ίδια στιγμή το μέτρο της ταχύτητας της σανίδας έχει μέτρο:
α) \[ωR\], β) \[\frac{ωR}{2}\], γ) \[2ωR\].
B) Αν σε χρόνο \[Δt\] το κέντρο μάζας του έχει μεταφερθεί κατά \[Δx_{cm}\], τότε η σανίδα μεταφέρεται στον ίδιο χρόνο κατά:
α) \[2Δx_{cm}\], β) \[Δx_{cm}\], γ) \[ \frac{ Δx_{cm} }{ 2 } \].
