1. Αν μια ομάδα ατόμων κινηθεί πάνω σε μια γέφυρα με κοινό βηματισμό τότε η γέφυρα εκτελεί εξαναγκασμένη μηχανική ταλάντωση. Η γέφυρα κινδυνεύει να καταστραφεί: 2. Σε μια φθίνουσα μηχανική ταλάντωση, η δύναμη που αντιστέκεται στην κίνηση είναι της μορφής \[F_{αν}=-bυ\] όπου \[υ\] η αλγεβρική τιμή της ταχύτητας και \[b\] μια θετική σταθερά. Στη διάρκεια μιας περιόδου το μέτρο της αντιτιθέμενης δύναμης \[F_{αν}\]: 3. Σύστημα ιδανικό ελατήριο-σώμα εκτελεί εξαναγκασμένη μηχανική ταλάντωση με τη βοήθεια διεγέρτη-τροχού. Ποιες από τις παρακάτω προτάσεις είναι σωστές; Όταν μεταβάλλω τη συχνότητα του διεγέρτη μεταβάλλεται: 4. Για τους δύο απλούς αρμονικούς ταλαντωτές του παρακάτω σχήματος ισχύει \[k_2=4k_1\] και \[m_2=\frac{m_1}{4}\]. Απομακρύνουμε τα σώματα κατά τη διεύθυνση του κεκλιμένου επιπέδου προς τα κάτω και τ’ αφήνω ελεύθερα. Κατά την απομάκρυνση των σωμάτων δαπανήσαμε και στα δύο την ίδια ενέργεια.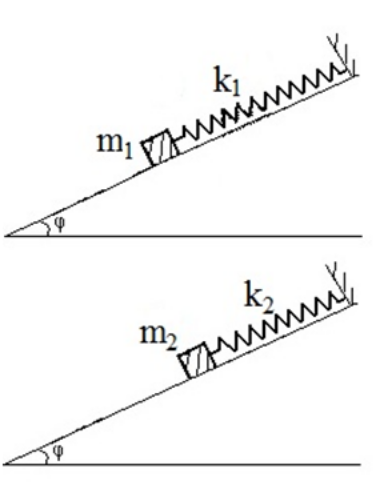
Α. Αν τα πλάτη των α.α.τ. είναι , αντίστοιχα, ισχύει γι’ αυτά:
α. \[Α_1=Α_2\].
β. \[Α_1=2Α_2\].
γ. \[Α_1=\frac{Α_2}{2}\].
δ. \[Α_1=\frac{Α_2}{4}\]
Β. Αν και είναι οι μέγιστες ορμές που αποκτούν τα σώματα κατά τη διάρκεια των α.α.τ., ισχύει:
α. \[p_{1,max}=p_{2,max}\].
β. \[ p_{1,max}=\frac{ p_{2,max} }{ 2}\].
γ. \[p_{1,max}=2p_{2,max}\].
δ. \[p_{1,max}=4p_{2,max}\].
5. Υλικό σημείο εκτελεί α.α.τ. πλάτους \[Α\] και ενέργειας \[Ε_Τ\]. Στο παρακάτω διάγραμμα φαίνεται η δυναμική ενέργεια \[U_T\] και η κινητική ενέργεια \[Κ\] της α.α.τ. σε συνάρτηση με την απομάκρυνση του σημείου απ’ τη Θ.Ι. του. Ποιες από τις παρακάτω προτάσεις είναι σωστές;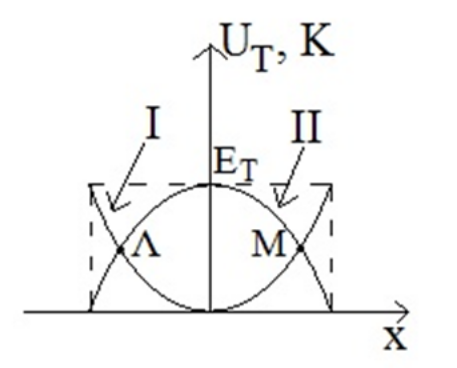
10. Σύστημα ιδανικό ελατήριο-σώμα βρίσκεται σε λείο οριζόντιο επίπεδο και ισορροπεί ακίνητο στη θέση που το ελατήριο έχει το φυσικό του μήκος. Στη θέση αυτή προσδίνω στο σώμα ταχύτητα \[υ_0\] που έχει τη διεύθυνση του άξονα του ελατηρίου. Το σύστημα αρχίζει να εκτελεί α.α.τ. Επαναλαμβάνω ακριβώς το ίδιο πείραμα διπλασιάζοντας το μέτρο της \[υ_0\]. Ποιες από τις παρακάτω προτάσεις είναι σωστές; 11. Ο δίσκος μάζας \[m_1\] του παρακάτω σχήματος εκτελεί α.α.τ. πλάτους \[Α_1=Δ\ell\] όπου \[Δ \ell\] η συσπείρωση του ελατηρίου στη Θ.Ι. του δίσκου. Όταν ο δίσκος βρίσκεται στην ανώτερη ακραία θέση του, τοποθετούμε σ’ αυτόν δεύτερο σώμα ίσης μάζας \[m_2=m_1\]. Το σύστημα των δύο σωμάτων εκτελεί α.α.τ. με πλάτος \[A_2\].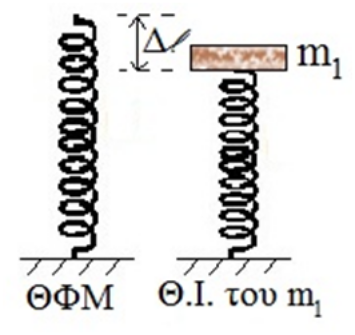
Α. Για τα πλάτη \[Α_1\, , \, Α_2\] ισχύει: α. \[Α_1=Α_2\]. β. \[Α_1=\frac{Α_2}{ 2 } \]. γ. \[Α_1=3Α_2\]. δ. \[Α_1=2Α_2\].
Β. Για τις μέγιστες δυναμικές ενέργειες του ελατηρίου \[U_{ελ,max,1}\, , \, U_{ελ,max,2}\] ισχύει:
α. \[U_{ελ,max,1}=U_{ελ,max,2}\].
β. \[U_{ελ,max,1}= \frac{ U_{ελ,max,2} }{ 4 }\].
γ. \[U_{ελ,max,1}=\frac{ U_{ ελ,max,2 } }{ 2 }\].
δ. \[U_{ελ,max,1}=\frac{ U_{ελ,max,2} }{ 16 }\].
14. Στο παρακάτω διάγραμμα φαίνεται η μεταβολή της δύναμης επαναφοράς που δέχεται ένας ταλαντωτής που εκτελεί α.α.τ. Ποιες από τις παρακάτω προτάσεις είναι σωστές;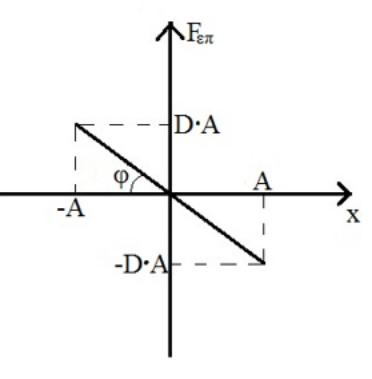
17. Στο παρακάτω διάγραμμα φαίνεται η μεταβολή της δυναμικής ενέργειας του ταλαντωτή σε συνάρτηση με το χρόνο. Ποιες από τις επόμενες προτάσεις είναι σωστές;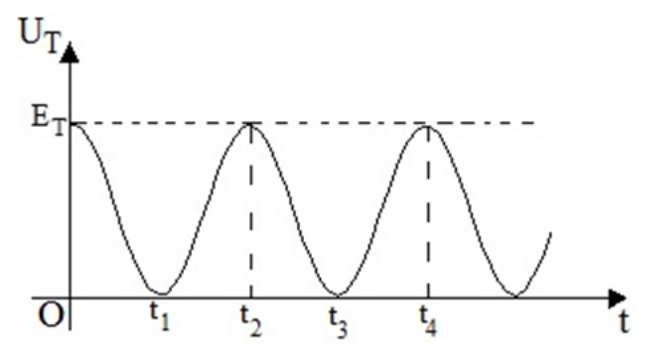
18. Τα σώματα \[Σ_1\], \[Σ_2\] του παρακάτω σχήματος ηρεμούν δεμένα στα κάτω άκρα πανομοιότυπων κατακόρυφων ελατηρίων που τα άλλα άκρα τους είναι ακλόνητα στερεωμένα σε οροφή. Τα σώματα έχουν μάζες \[m_1\] και \[m_2=2m_1\] αντίστοιχα. Εκτρέπω τα σώματα κατακόρυφα προς τα πάνω μέχρι τα δύο ελατήρια ν’ αποκτήσουν το φυσικό τους μήκος και απ’ τη θέση αυτή τα αφήνω ελεύθερα να κινηθούν. Τα σώματα εκτελούν α.α.τ. Ο λόγος των μέγιστων δυναμικών ενεργειών των δύο ελατηρίων κατά τη διάρκεια των ταλαντώσεων είναι: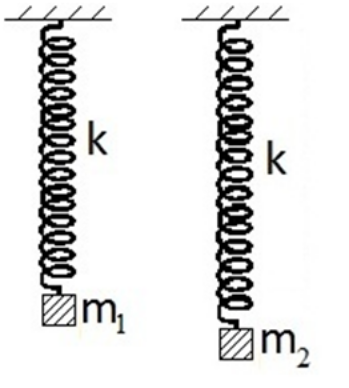
20. Στο παρακάτω διάγραμμα φαίνονται οι γραφικές παραστάσεις της μεταβολής των φάσεων σε συνάρτηση με το χρόνο για δύο απλούς αρμονικούς ταλαντωτές. Ποιες από τις παρακάτω προτάσεις είναι σωστές;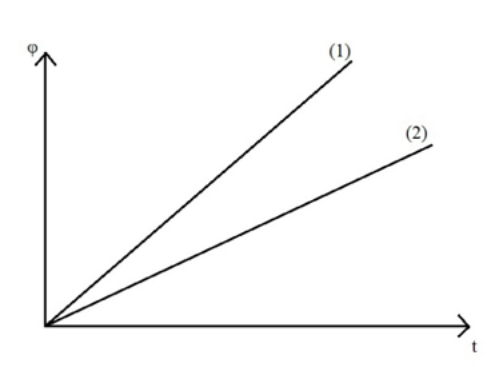
23. Σώμα εκτελεί α.α.τ. Ποιες από τις παρακάτω προτάσεις είναι σωστές; Η διαφορά φάσης: 24. Σύστημα ιδανικό ελατήριο-σώμα εκτελεί εξαναγκασμένη μηχανική ταλάντωση με τη βοήθεια τροχού-διεγέρτη. Η ιδιοσυχνότητα του συστήματος είναι \[f_0=60\, Hz\]. Αυξάνω αργά τη συχνότητα του διεγέρτη απ’ την τιμή \[f_1=50\, Hz\] ως την τιμή \[f_2=65\, Hz\]. Κατά την αύξηση αυτή: 25. Στο παρακάτω σχήμα φαίνεται η μεταβολή της δυναμικής και της κινητικής ενέργειας ενός απλού αρμονικού ταλαντωτή με το χρόνο. Η αρχική φάση της ταλάντωσης είναι \[φ_0=\frac{π}{2}\]. Ποιες από τις παρακάτω προτάσεις είναι σωστές;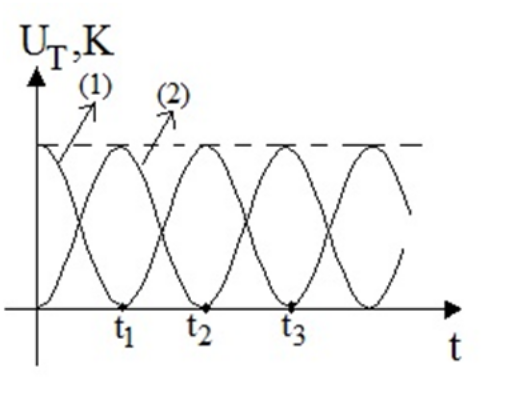
27. Στο θάλαμο της πειραματικής διάταξης για τη μελέτη μιας φθίνουσας ταλάντωσης τοποθετούμε ορισμένη ποσότητα αέρα μέσω της αεραντλίας και θέτουμε το σύστημα ελατήριο-σώμα σε ταλάντωση. Αν η πίεση του αέρα στο θάλαμο παραμένει συνεχώς σταθερή, ποιες από τις παρακάτω προτάσεις είναι σωστές; 30. Σε μια φθίνουσα μηχανική ταλάντωση περιόδου \[Τ\], το πλάτος της μεταβάλλεται με το χρόνο σύμφωνα με τη σχέση \[Α=Α_0\, e^{-Λt}\] όπου \[Λ\] θετική σταθερά. Αν \[Ε_{Τ,κ}\] και \[Ε_{Τ,κ+1}\] η ενέργεια της ταλάντωσης τις χρονικές στιγμές \[t_1=κT\] και \[t_2=(κ+1)T\] (όπου \[κ\] θετικός ακέραιος), ποιες από τις παρακάτω προτάσεις είναι σωστές; Για το πηλίκο \[ \frac{ Ε_{Τ,κ} } { Ε_{Τ,κ+1} } \] ισχύει ότι: 