1. Ο αγωγός (1) του παρακάτω σχήματος έχει σχήμα τεταρτοκυκλίου ακτίνας \[r\] και κέντρου Κ. Ο αγωγός αυτός διαρρέεται από ρεύμα έντασης \[Ι\] που η φορά της φαίνεται στο σχήμα. Ο αγωγός (2) είναι κυκλικό τμήμα ίδιας ακτίνας \[r\] και ίδιου κέντρου που αντιστοιχεί σε επίκεντρη γωνία \[θ=30^0\]. Ο αγωγός (2) διαρρέεται από ρεύμα \[Ι'\]. Τα επίπεδα των δύο αγωγών ταυτίζονται με αυτό της σελίδας. Αν στο κέντρο Κ η ολική ένταση των μαγνητικών πεδίων των δύο αγωγών είναι μηδενική, τότε ο λόγος \[\frac{Ι'}{ Ι} \] είναι: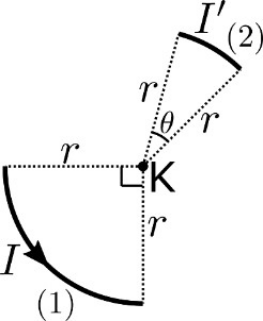
2. Ποια απ’ τις παρακάτω προτάσεις είναι σωστή; Αν μέσα σ’ ένα ομογενές μαγνητικό πεδίο τοποθετήσω σιδερένιο δακτύλιο τότε: 3. Ποια απ’ τις παρακάτω προτάσεις είναι σωστή; Στο παρακάτω σχήμα το στοιχειώδες τμήμα \[Δ\ell\] ρευματοφόρου αγωγού που διαρρέεται από ρεύμα έντασης \[Ι\] δημιουργεί στο σημείο Α του επιπέδου της σελίδας ένταση \[Δ\vec{B}\]. Ο αγωγός βρίσκεται και αυτός πάνω στο επίπεδο της σελίδας. Το μέτρο της έντασης \[ΔΒ\] είναι: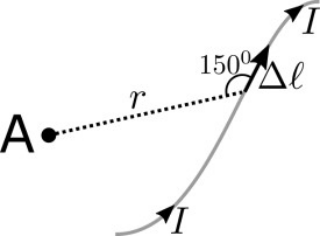
4. Ποιες απ’ τις παρακάτω προτάσεις είναι σωστές; 5. Πρωτόνιο εισέρχεται σε ομογενές μαγνητικό πεδίο με ταχύτητα \[ \vec{υ} \] που είναι κάθετη στις δυναμικές γραμμές του. Το πρωτόνιο εκτελεί κυκλική κίνηση ακτίνας \[R_1\] και περιόδου \[Τ_1\]. Αν το πρωτόνιο εισέρχονταν στο ίδιο πεδίο με ταχύτητα ίδιας κατεύθυνσης αλλά διπλάσιου μέτρου τότε θα εκτελούσε κυκλική κίνηση ακτίνας \[R_2\] και περιόδου \[Τ_2\]. Ποια απ’ τις παρακάτω σχέσεις είναι σωστή; 6. Ποια απ’ τις παρακάτω προτάσεις είναι σωστή; Ο Νόμος του Ampere μπορεί να εφαρμοστεί για την εύρεση της έντασης: 7. Ποιες απ’ τις παρακάτω προτάσεις είναι σωστές; Οι κυκλικές δυναμικές γραμμές του μαγνητικού πεδίου ενός ευθύγραμμου ρευματοφόρου αγωγού απείρου μήκους: 8. Σε χώρο που αμελούνται οι βαρυτικές δυνάμεις ένα σωματίδιο κινείται ευθύγραμμα και ομαλά. Ποιες απ’ τις παρακάτω προτάσεις είναι σωστές; 10. Ποιες από τις παρακάτω προτάσεις είναι σωστές; Το διάνυσμα της έντασης του μαγνητικού πεδίου στο κέντρο κυκλικού ρευματοφόρου αγωγού: 11. Φορτισμένο σωματίδιο μάζας \[m\], φορτίου \[q\] εισέρχεται σε ομογενές μαγνητικό πεδίο έντασης μέτρου \[B\] με ταχύτητα μέτρου \[υ\] κάθετα στις δυναμικές γραμμές. Ποιες από τις παρακάτω προτάσεις είναι σωστές; Για το ρυθμό μεταβολής της κινητικής ενέργειας \[\frac{ΔΚ}{Δt}\] του σωματιδίου και το μέτρο του ρυθμού μεταβολής της ορμής του \[\left| \frac{Δ\vec{p} }{ Δt } \right| \] αν το σωματίδιο δέχεται μόνο τη δύναμη Lorentz \[F_{Lo}\] απ’ το πεδίο ισχύει: 13. Φορτισμένο σωματίδιο εκτελεί ομαλή κυκλική κίνηση μέσα σε ομογενές μαγνητικό πεδίο και επιδρά σ’ αυτό μόνο η δύναμη Lorentz που δέχεται απ’ το πεδίο. Ποιες απ’ τις παρακάτω προτάσεις είναι σωστές; 15. Στο πείραμα του Thomson μέσα στον καθοδικό σωλήνα απ’ την πυρακτωμένη κάθοδο εκπέμπονται ηλεκτρόνια που επιταχύνονται υπό τάση \[V\] που δημιουργείται μεταξύ της καθόδου και των δύο ανόδων Α, Α΄. Έτσι δημιουργείται μια δέσμη ηλεκτρονίων που κατόπιν περνούν μέσα από φίλτρο ταχυτήτων της διάταξης χωρίς ν’ αποκλίνουν της αρχικής τους πορείας και καταλήγουν στη φθορίζουσα οθόνη. Αν τετραπλασιάσουμε την τάση που επιταχύνει τα ηλεκτρόνια, για να μην αποκλίνει η δέσμη μέσα στο φίλτρο ταχυτήτων πρέπει: 19. Το σωληνοειδές Σ του παρακάτω σχήματος έχει συνδεθεί υπό σταθερή τάση \[V\] και διαρρέεται υπό σταθερό ρεύμα \[Ι\]. Η ένταση του μαγνητικού πεδίου στο κέντρο του έχει μέτρο \[Β_Κ\]. Κόβω το σωληνοειδές σε δύο ίσα μέρη \[Σ_1,\, Σ_2\] και στα άκρα του \[Σ_1\] εφαρμόζω την ίδια σταθερή τάση \[V\]. Ποιες απ’ τις παρακάτω προτάσεις είναι σωστές;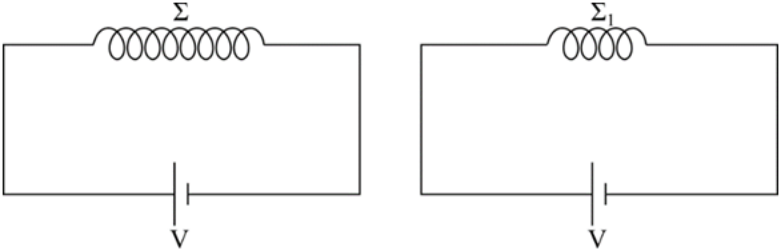
20. Στο παρακάτω σχήμα φαίνονται χωρίς κλίμακα οι κυκλικές τροχιές ενός πρωτονίου και ενός ηλεκτρονίου μέσα στο ίδιο ομογενές μαγνητικό πεδίο. Τα σωματίδια αυτά δέχονται μόνο τη δύναμη Lorentz απ’ το μαγνητικό πεδίο και έχουν ίσες κατά μέτρο ταχύτητες. Πρέπει να γνωρίζετε ότι το πρωτόνιο και το ηλεκτρόνιο έχουν αντίθετα φορτία και ότι η μάζα του πρωτονίου είναι \[1836\] φορές μεγαλύτερη απ’ αυτήν του ηλεκτρονίου. Ποιες από τις παρακάτω προτάσεις είναι σωστές;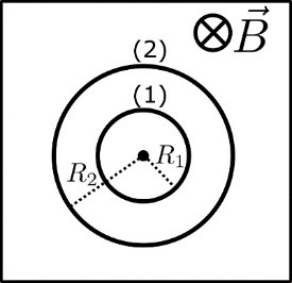
21. Το πλαίσιο ΚΛΜΝ του παρακάτω σχήματος είναι σχήματος ορθογωνίου παραλληλογράμμου πλευρών \[ΚΛ=α\] και \[ΛΜ=2α\] αντίστοιχα και διαρρέεται από ρεύμα έντασης \[I\] που έχει τη φορά των δεικτών του ρολογιού. Το πλαίσιο βρίσκεται πάνω σε οριζόντιο λείο επίπεδο και το μισό βρίσκεται μέσα σε κατακόρυφο ομογενές μαγνητικό πεδίο έντασης μέτρου \[B\]. Στο ίδιο οριζόντιο επίπεδο βρίσκεται ευθύγραμμος ρευματοφόρος αγωγός (1) που διαρρέεται από ρεύμα έντασης \[I_1=I\] που είναι ομόρροπο με το ρεύμα που διαρρέει την πλευρά ΚΛ. Ο αγωγός (1) απέχει \[α\] απ’ την πλευρά ΚΛ του πλαισίου. Το πλαίσιο αφήνεται ελεύθερο να κινηθεί και παρατηρούμε ότι παραμένει ακίνητο. Η μαγνητική διαπερατότητα του κενού είναι \[μ_0\]. Για το μέτρο και τη φορά της \[\vec{B}\] του ομογενούς μαγνητικού πεδίου ισχύει: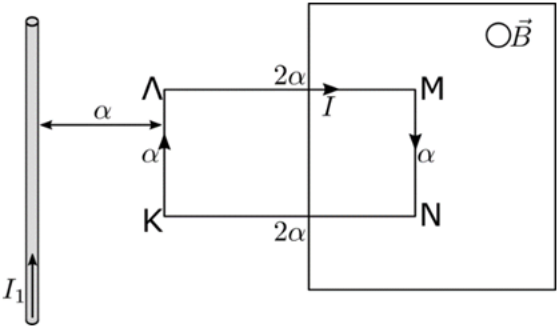
23. Στο παρακάτω σχήμα φαίνονται διαγράμματα που αναφέρονται στο μαγνητικό πεδίο ευθύγραμμου ρευματοφόρου αγωγού απείρου μήκους. Ποιες από τις παρακάτω προτάσεις είναι σωστές;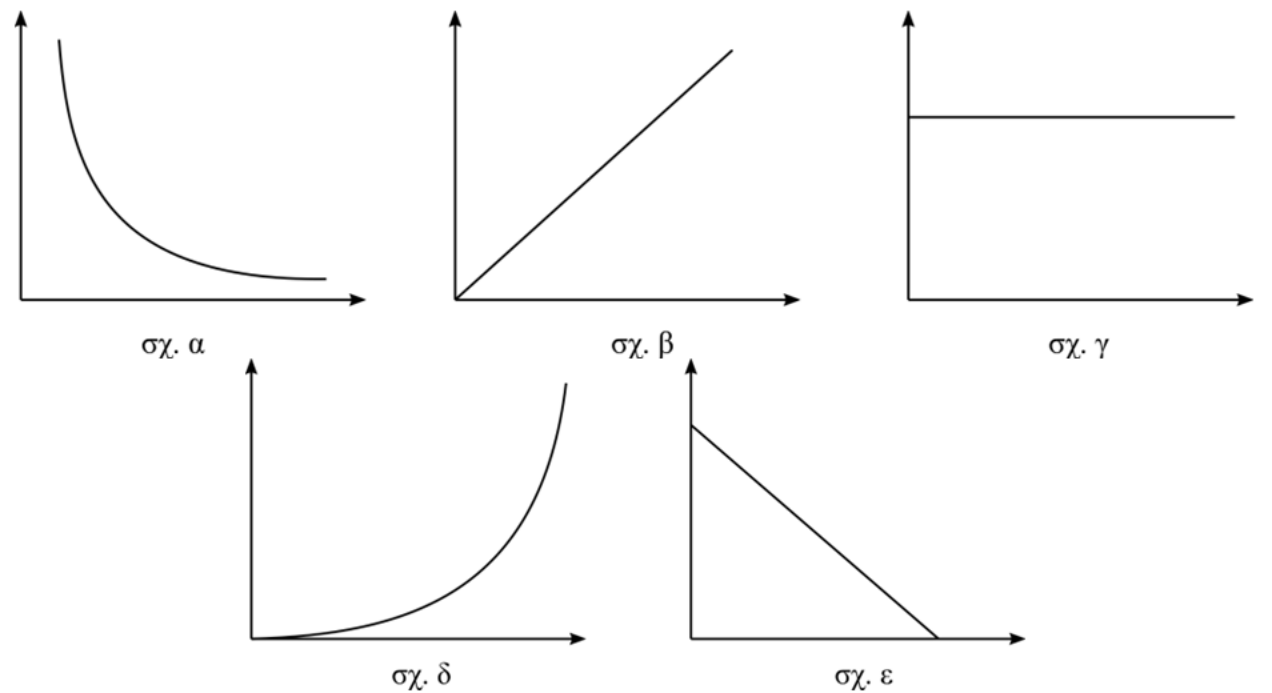
27. Ένα πρωτόνιο \[p\] μάζας \[m_p\] και φορτίου \[e\] και ένα σωμάτιο \[α\] μάζας \[m_α=4m_p\] και φορτίου \[q_α=2e\] όπου \[e\] το στοιχειώδες θετικό φορτίο εισέρχονται ταυτόχρονα απ’ το ίδιο σημείο Γ με ταχύτητες \[\vec{υ}_α\, , \, \vec{υ}_p \] σε ομογενές μαγνητικό πεδίο έντασης \[\vec{Β}\] έτσι ώστε οι ταχύτητές τους να είναι κάθετες στις δυναμικές γραμμές του πεδίου και στο όριό του που είναι η ευθεία \[xx'\] όπως φαίνεται στο παρακάτω σχήμα. Τα σωματίδια δέχονται μόνο τις δυνάμεις απ’ το μαγνητικό πεδίο που εκτείνεται σε μεγάλη απόσταση πάνω απ’ το όριο του \[xx'\]. Κατά την είσοδό τους στο πεδίο έχουν ίσες κινητικές ενέργειες \[(K_p=K_α )\]. Για το λόγo των ακτίνων τους \[\frac{R_p }{ R_α}\] και το λόγο των συχνοτήτων τους \[\frac{f_p }{ f_α }\] ισχύει: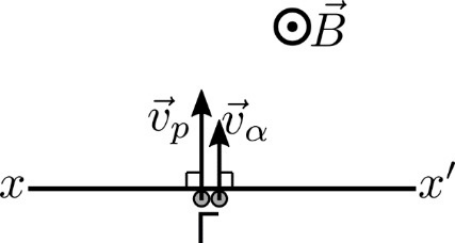
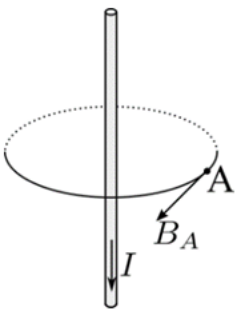
28. Στο παρακάτω σχήμα φαίνεται το διάνυσμα της έντασης του μαγνητικού πεδίου ευθύγραμμου ρευματοφόρου αγωγού απείρου μήκους που διαρρέεται από ρεύμα σταθερής έντασης \[Ι\] σ’ ένα σημείο Α του πεδίου αυτού. Ποιες από τις παρακάτω προτάσεις είναι σωστές;