2. Στο παρακάτω σχήμα φαίνονται δύο κλειστές διαδρομές \[S_1\, , \, S_2\] σχήματος ομοεπίπεδων τετραγώνων πλευράς \[α\, ,\, 2α\] αντίστοιχα και οι φορές διαγραφής. Η διαδρομή \[S_1\] περικλείει τρεις ευθύγραμμους παράλληλους αγωγούς που διαρρέονται από ομόρροπα ρεύματα ίδιας έντασης \[Ι\] το καθένα. Η διεύθυνση των αγωγών είναι κάθετη στο επίπεδο των δύο επιφανειών. Για να γίνει το άθροισμα \[∑B\cdot Δ\ell \cdot συνφ\] στη διαδρομή \[S_2\] ίσο με το μηδέν χωρίς ν’ αλλάξει το αντίστοιχο άθροισμα στη διαδρομή \[S_1\] πρέπει: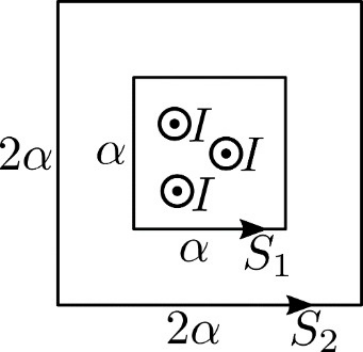
4. Ποιες απ’ τις επόμενες προτάσεις είναι σωστές; Σε ένα βρόχο το άθροισμα \[∑ B \cdot Δ\ell \cdot συνθ\] είναι μηδενικό, τότε: 5. Φορτισμένο σωματίδιο εισέρχεται σε ομογενές μαγνητικό πεδίο με ταχύτητα \[\vec{υ}\] που σχηματίζει γωνία \[φ\] (\[ 0 < φ < 90^0 \]) με τις δυναμικές γραμμές του πεδίου και δέχεται δύναμη μόνο απ’ αυτό. Το σωματίδιο εκτελεί ελικοειδή τροχιά. Ποιες απ’ τις παρακάτω προτάσεις είναι σωστές; 8. Ο αγωγός του παρακάτω σχήματος διαρρέεται από ρεύμα έντασης \[Ι\]. Ένα στοιχειώδες τμήμα \[Δ\ell\] του αγωγού έχει αποστάσεις \[r_1\, , \, r_2\] απ’ τα σημεία Α, Γ αντίστοιχα. Οι αποστάσεις αυτές είναι κάθετες μεταξύ τους και ίσες \[(r_1=r_2)\]. Tα διανύσματα \[Δ\vec{\ell}\, , \, \vec{r}_1\] σχηματίζουν μεταξύ τους γωνία \[θ_1=30^0\]. Τότε για τα διανύσματα των εντάσεων \[Δ\vec{Β}_A\, , \, Δ\vec{B}_Γ\] που οφείλονται στο στοιχειώδες τμήμα \[Δ\ell\] στα σημεία Α, Γ αντίστοιχα ισχύει: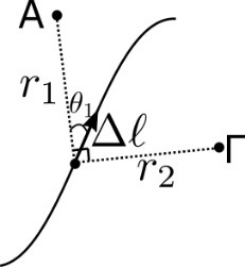
10. Οι δύο παράλληλοι ρευματοφόροι αγωγοί \[(1),\, (2)\] του παρακάτω σχήματος βρίσκονται ακλόνητοι πάνω σε λείο οριζόντιο μονωτικό επίπεδο και διαρρέονται από αντίρροπα ρεύματα \[Ι_1,\, Ι_2\] αντίστοιχα με \[I_1 < I_2\]. Ποια απ’ τις παρακάτω προτάσεις είναι σωστή; Η θέση που μπορώ να τοποθετήσω έναν τρίτο παράλληλο ρευματοφόρο αγωγό \[(3)\] ώστε αυτός να ισορροπεί είναι: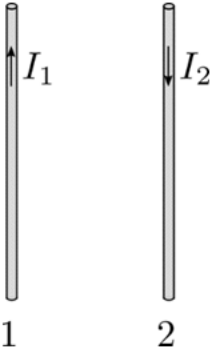
14. Το πλαίσιο ΚΛΜΝ με πλευρές \[α,\, γ\] του παρακάτω σχήματος είναι προσδεμένο απ’ το μέσο της πλευράς του ΚΛ απ’ το άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς \[k\] που το άλλο άκρο του είναι προσδεμένο σε οροφή. Το πλαίσιο διαρρέεται από ρεύμα έντασης \[I\] που η φορά του φαίνεται στο σχήμα ενώ βρίσκεται κατά ένα μέρος του (κάτω απ’ την ευθεία ε) μέσα σε οριζόντιο ομογενές μαγνητικό πεδίο έντασης μέτρου \[B_1\] με φορά προς τον αναγνώστη, ενώ το υπόλοιπο είναι εκτός πεδίου (σχ. α). Το πλαίσιο ισορροπεί ακίνητο και το ελατήριο είναι επιμηκυμένο κατά \[Δ\ell\]. Δημιουργούμε δεύτερο οριζόντιο ομογενές μαγνητικό πεδίο έντασης μέτρου \[B_2\] αντίρροπης της \[B_1\]. Το πεδίο έντασης \[Β_2\] αυτό εκτείνεται πάνω απ’ την ευθεία ε (σχ. β). Τώρα το πλαίσιο ισορροπεί με το ελατήριο να είναι παραμορφωμένο κατά \[1,5Δ\ell\]. Το βάρος του πλαισίου έχει μέτρο \[w=\frac{ B_1 I α }{ 2 } \].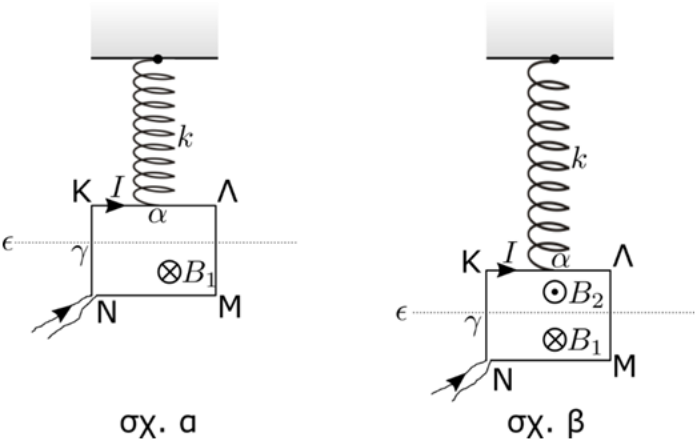
Α) Για τα μέτρα των εντάσεων των δύο μαγνητικών πεδίων ισχύει:
α) \[B_1=\frac{4}{3} B_2\],
β) \[B_1=\frac{3}{2} B_2\],
γ) \[Β_1=\frac{Β_2}{2}\].
Β) Αν αντιστρέψω τη φορά της έντασης \[Β_2\], τότε το πλαίσιο θα ισορροπεί όταν το ελατήριο έχει επιμήκυνση \[Δ \ell'\] που είναι ίση με:
α) \[Δ \ell \], β) \[0,75\, Δ\ell \], γ) \[0,5\, Δ\ell\].
16. Σωματίδιο μάζας \[m\] και φορτίου \[q\] εισέρχεται μέσα σε ομογενές μαγνητικό πεδίο έντασης \[\vec{B}\] με ταχύτητα \[\vec{υ}\] που σχηματίζει γωνία \[φ\] με τις δυναμικές του γραμμές \[(0 < φ < 90^0)\]. Ποια απ’ τις παρακάτω προτάσεις είναι σωστή; Αν αυξήσω τη γωνία \[φ\] κατά την είσοδο του σωματιδίου στο πεδίο διατηρώντας την μεταξύ των τιμών \[0 < φ < 90^0\] τότε: 19. Ένα πρωτόνιο μάζας \[m_p\] και φορτίου \[e\] (στοιχειώδες φορτίο) και ένας πυρήνας ηλίου μάζας \[4m_p\] και φορτίου \[2e\] εκτελούν κυκλικές τροχιές με ακτίνες \[R_p\, , \, R_α\] αντίστοιχα με ίσες κατά μέτρο ταχύτητες. Ποιες απ’ τις παρακάτω προτάσεις είναι σωστές;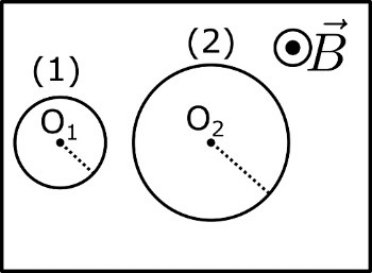
21. Τρία σωματίδια (1), (2), (3) μπαίνουν ταυτόχρονα στο ίδιο ομογενές μαγνητικό πεδίο κάθετα στο όριό του (πλευρά ΑΕ) και στις δυναμικές γραμμές του με ταχύτητες ίσων μέτρων. Για τα φορτία των σωματιδίων (2), (3) ισχύει \[ |q_2 |=|q_3 |=|q|\] και οι μάζες τους είναι \[m_2\, , \, m_3\] αντίστοιχα. Οι βαρυτικές δυνάμεις θεωρούνται αμελητέες. Στο παρακάτω σχήμα φαίνονται οι τροχιές των σωματιδίων μέσα στο πεδίο. Ποιες από τις παρακάτω προτάσεις είναι σωστές;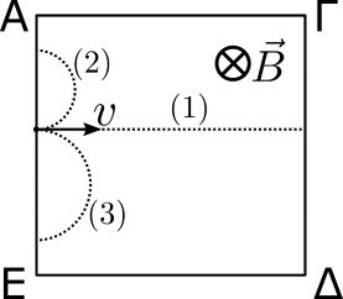
22. Ο αγωγός του παρακάτω σχήματος ισορροπεί οριζόντιος μέσα σε οριζόντιο ομογενές μαγνητικό πεδίο έντασης \[\vec{B}\]. Ο αγωγός ακουμπά χωρίς τριβές σε δύο αγώγιμες κατακόρυφες ράβδους που στα άκρα τους έχουμε συνδέσει ηλεκτρική πηγή. Ποιες απ’ τις παρακάτω προτάσεις είναι σωστές;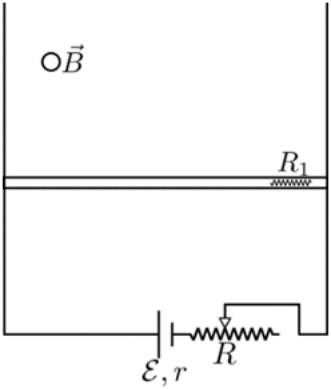
23. Τα δύο φορτισμένα σωματίδια του παρακάτω σχήματος έχουν φορτία \[ q_1 \, , \, q_2\] με ίσες μάζες \[m_1 = m_2\] αντίστοιχα και εκτελούν ομαλή κυκλική κίνηση ακτίνων \[ R_1 \, , \, R_2\] μέσα στο ίδιο ομογενές μαγνητικό πεδίο έντασης \[\vec{B}\] μόνο με την επίδραση των δυνάμεων που δέχονται απ’ το μαγνητικό πεδίο. Οι κινητικές ενέργειες των δύο σωματιδίων είναι ίσες \[Κ_1 = Κ_2\]. Για τα πρόσημα και τις απόλυτες τιμές των δύο φορτίων τους ισχύει: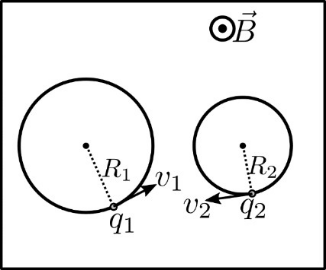
24. Φορτισμένο σωματίδιο μάζας \[m\] και φορτίου \[q\] εισέρχεται σε ομογενές μαγνητικό πεδίο έντασης \[\vec{B}\] με ταχύτητα \[\vec{υ}\] που σχηματίζει γωνία \[φ=60^0\] με τις δυναμικές γραμμές του πεδίου. Το σωματίδιο εκτελεί ελικοειδή κίνηση και η μόνη δύναμη που δέχεται είναι αυτή απ’ το μαγνητικό πεδίο. Ποιες απ’ τις επόμενες προτάσεις είναι σωστές; 26. Στο πείραμα του Thomson τα ηλεκτρόνια που εκπέμπει η πυρακτωμένη κάθοδος επιταχύνονται υπό μια τάση \[V\] και η δέσμη ηλεκτρονίων εισέρχεται σε επιλογέα ταχυτήτων που το μαγνητικό και ηλεκτρικό πεδίο του έχουν εντάσεις μέτρων \[B\] και \[E\] αντίστοιχα. Ποιες απ’ τις παρακάτω προτάσεις είναι σωστές; 28. Δύο φορτισμένα σωματίδια (1), (2) έχουν ίσες κατά μέτρο ορμές, μάζες \[m_1=2m_2\] και ίσα φορτία. Τα σωματίδια εισέρχονται στο ίδιο ομογενές μαγνητικό πεδίο και εκτελούν σ’ αυτό ομαλή κυκλική κίνηση με ακτίνες \[R_1, R_2\] και περιόδων \[T_1, T_2\] αντίστοιχα με την επίδραση μόνο της δύναμης Lorentz που δέχονται απ’ το πεδίο. Ποια απ’ τις παρακάτω προτάσεις είναι σωστή; Για τις ακτίνες και τις περιόδους των κυκλικών κινήσεων των δύο σωματιδίων ισχύει: 