11. Τα πανομοιότυπα τετραγωνικά πλαίσια (1), (2) του παρακάτω σχήματος έχουν εμβαδά \[S\] αποτελούνται από \[Ν\] σπείρες και βρίσκονται μέσα σε ομογενές μαγνητικό πεδίο έντασης μέτρου \[B\]. Το πλαίσιο (1) είναι αρχικά κάθετο στις δυναμικές γραμμές του μαγνητικού πεδίου ενώ το πλαίσιο (2) είναι παράλληλο στις δυναμικές του γραμμές. Στρέφουμε τα πλαίσια κατά γωνία \[30^0\] κατά τη φορά που φαίνεται στο σχήμα. Αν \[ΔΦ_1\] και \[ΔΦ_2\] είναι οι μεταβολές των μαγνητικών ροών μιας σπείρας του πλαισίου (1) και του πλαισίου (2) αντίστοιχα, τότε ισχύει: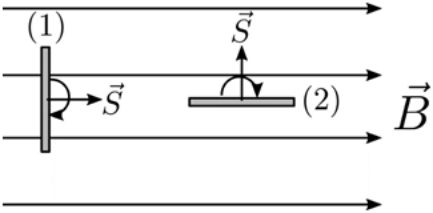
15. Η αγώγιμη ράβδος ΟΑ μήκους \[\ell\] στρέφεται γύρω από άξονα που διέρχεται απ’ το Ο και είναι κάθετη σ’ αυτήν με σταθερή γωνιακή ταχύτητα \[ω\]. Η ράβδος βρίσκεται σε ομογενές μαγνητικό πεδίο έντασης \[Β\] που οι δυναμικές γραμμές του είναι παράλληλες στον άξονα περιστροφής της. Ποιες από τις παρακάτω προτάσεις είναι σωστές;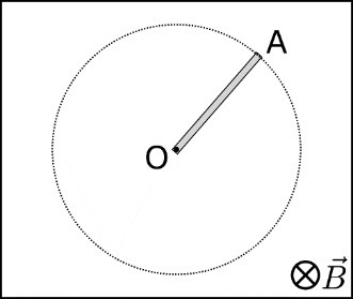
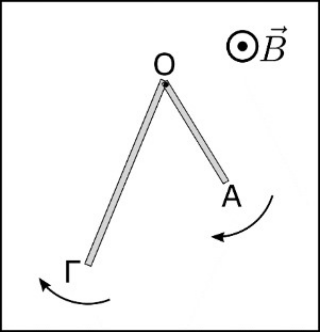
16. Ποια απ’ τις επόμενες προτάσεις είναι σωστή; Σύμφωνα με το νόμο της επαγωγής (Faraday), η ΗΕΔ από επαγωγή που δημιουργείται σ’ ένα πηνίο: 17. Δύο ευθύγραμμοι λεπτοί μεταλλικοί αγωγοί ΟΑ και ΟΓ στρέφονται στο ίδιο επίπεδο γύρω από άξονα που διέρχεται απ’ το κοινό άκρο Ο και είναι κάθετος σ’ αυτούς με την ίδια σταθερή γωνιακή ταχύτητα κατά μέτρο και φορά. Οι αγωγοί έχουν μήκη \[\ell_{OA}\, , \, \ell_{ΟΓ} \] αντίστοιχα με \[\ell_{OA}=\frac{\ell_{ΟΓ} }{ 2 }\] και βρίσκονται σε ομογενές μαγνητικό πεδίο έντασης \[\vec{B}\] που οι δυναμικές γραμμές του είναι κάθετες στο επίπεδο περιστροφής τους. Ποια απ’ τις επόμενες προτάσεις είναι σωστή; Για τις επαγωγικές ΗΕΔ που δημιουργούνται στους αγωγούς ισχύει: 18. Αντιστάτης αντίστασης \[R\] συνδέεται από εναλλασσόμενη τάση της μορφής \[v=V\, ημωt\] και διαρρέεται από εναλλασσόμενο ρεύμα στιγμιαίας έντασης \[i\]. Ποιες από τις παρακάτω προτάσεις είναι σωστές; 20. Ο μεταλλικός δακτύλιος του παρακάτω σχήματος είναι ανοικτός και κρέμεται με τη βοήθεια αβαρούς μονωτικού νήματος έτσι ώστε το επίπεδό του να παραμένει κατακόρυφο. Πλησιάζω στο δακτύλιο ραβδόμορφο μαγνήτη που ο άξονάς του ταυτίζεται με τον οριζόντιο άξονα που διέρχεται απ’ το κέντρο του δακτυλίου. Στη διάρκεια της προσέγγισης του μαγνήτη στο δακτύλιο: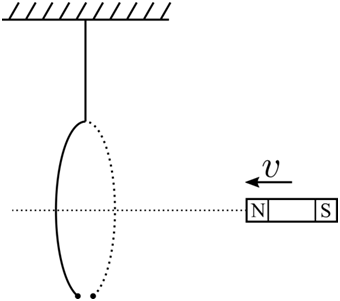
24. Η ΗΕΔ από αυτεπαγωγή στα άκρα ενός πηνίου είναι: 27. Η ράβδος ΟΓ του παρακάτω σχήματος έχει μήκος \[ \ell \] και αποτελείται από δύο ίσα τμήματα. Το ένα τμήμα ΟΑ είναι από πλαστικό και το άλλο τμήμα ΑΓ είναι από μέταλλο. Η ράβδος στρέφεται με σταθερή γωνιακή ταχύτητα μέτρου \[ω\] ως προς άξονα κάθετο σ’ αυτήν, που διέρχεται απ’ το άκρο της Ο. Η ράβδος βρίσκεται σε ομογενές μαγνητικό πεδίο έντασης μέτρου \[Β\] που οι γραμμές του είναι παράλληλες στον άξονα περιστροφής. Ποια απ’ τις παρακάτω προτάσεις είναι σωστή; Η επαγωγική ΗΕΔ που εμφανίζεται στο τμήμα ΑΓ της ράβδου είναι ίση με: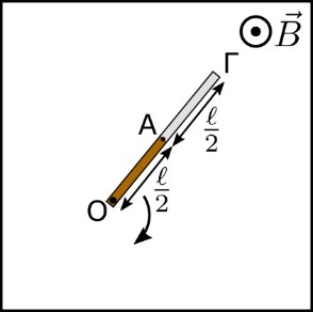
30. Οι οριζόντιοι ευθύγραμμοι αγωγοί ΟΓ και ΟΑ έχουν μήκη \[\ell\] και \[\frac{\ell }{ 2 }\] αντίστοιχα και στρέφονται στο ίδιο οριζόντιο επίπεδο με ίδια σταθερή γωνιακή ταχύτητα μέτρου \[ω\] γύρω από κατακόρυφο άξονα που διέρχεται απ’ το κοινό τους άκρο Ο. Το σύστημα των δύο αγωγών βρίσκεται μέσα σε κατακόρυφο ομογενές μαγνητικό πεδίο έντασης μέτρου \[Β\]. Η διαφορά δυναμικού \[V_{ΓΑ}\] μεταξύ των σημείων Γ, Α είναι ίση με: