4. Ποιες από τις παρακάτω προτάσεις είναι σωστές; 10. Δύο σφαίρες κινούνται με ταχύτητες \[\vec {υ}_1\] και \[\vec {υ}_2\] και συγκρούονται κεντρικά και ελαστικά. Αν μετά την κρούση οι δύο σφαίρες κινούνται με ταχύτητες \[\vec {υ}_1'\] και \[\vec {υ}_2'\] τότε ισχύει: 17. Μια σφαίρα πολύ μικρής μάζας κινείται με ταχύτητα \[\vec{υ}\] και συγκρούεται κεντρικά και ελαστικά με άλλη ακίνητη σφαίρα πολύ μεγαλύτερης μάζας. Ποιες από τις επόμενες προτάσεις είναι σωστές; 18. Κατά την κεντρική πλαστική κρούση μιας σφαίρας \[Σ_1\] μάζας \[m_1\] που κτυπάει με ταχύτητα \[υ_0\] σε ακίνητη σφαίρα \[Σ_2\] μάζας \[m_2\]. Να επιλέξετε τις σωστές από τις παρακάτω προτάσεις. 21. Μια σφαίρα Α μάζας \[m_1\] κινείται με ταχύτητα μέτρου \[12\frac{m}{s}\] και συγκρούεται κεντρικά και ελαστικά με ακίνητη σφαίρα Β διπλάσιας μάζας. Ποια από τις επόμενες προτάσεις είναι η σωστή: 22. Κατά την μετωπική ελαστική κρούση μιας σφαίρας \[Σ_1\] μάζας \[m_1\] που χτυπάει με ταχύτητα \[υ_0\] σε ακίνητη σφαίρα \[Σ_2\] μάζας \[m_2\], 25. Θεωρούμε ως σύστημα τα δύο σώματα \[Σ_1,Σ_2\] και το νήμα. Τα σώματα έχουν μάζες (\[m_1=m\]) και (\[m_2=4m\]) αντίστοιχα. Ασκούμε σταθερή οριζόντια δύναμη και τα κινούμε στο λείο οριζόντιο επίπεδο. Το νήμα είναι αβαρές, μη εκτατό και διαρκώς τεντωμένο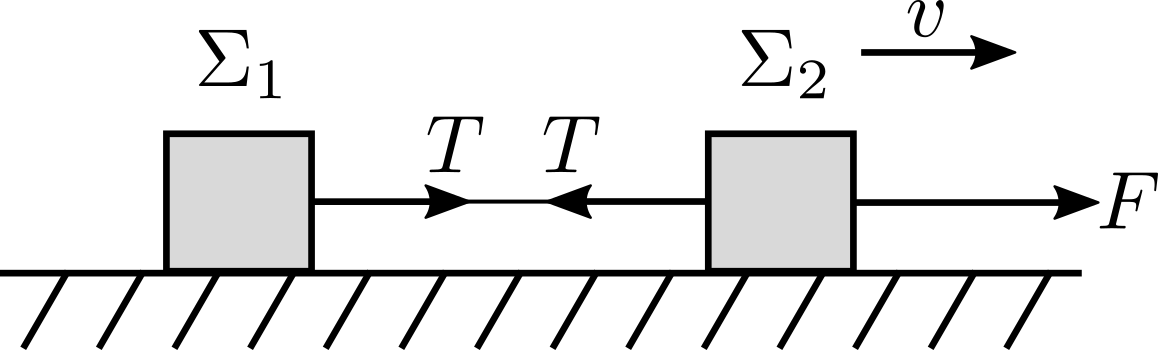
26. Μια κινούμενη ελαστική σφαίρα Α κινείται με ταχύτητα \[υ_1\] και συγκρούεται μετωπικά και ελαστικά με άλλη αρχικά ακίνητη σφαίρα Β. Ποιες από τις παρακάτω προτάσεις είναι σωστές;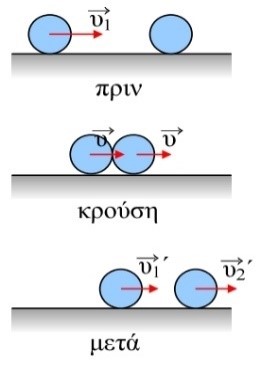
29. Ποιο από τα ακόλουθα σώματα έχει τη μεγαλύτερη κατά μέτρο ορμή; 