1. Φορτισμένο σωματίδιο μάζας \[m\], φορτίου \[q\] εισέρχεται σε ομογενές μαγνητικό πεδίο έντασης μέτρου \[B\] με ταχύτητα μέτρου \[υ\] κάθετα στις δυναμικές γραμμές. Ποιες από τις παρακάτω προτάσεις είναι σωστές; Για το ρυθμό μεταβολής της κινητικής ενέργειας \[\frac{ΔΚ}{Δt}\] του σωματιδίου και το μέτρο του ρυθμού μεταβολής της ορμής του \[\left| \frac{Δ\vec{p} }{ Δt } \right| \] αν το σωματίδιο δέχεται μόνο τη δύναμη Lorentz \[F_{Lo}\] απ’ το πεδίο ισχύει: 8. Θετικά φορτισμένο σωματίδιο \[(1)\] εισέρχεται σε φίλτρο ταχυτήτων και δεν αποκλίνει της πορείας του μέσα σ’ αυτό. Δεύτερο σωματίδιο \[(2)\] που έχει ίδια ταχύτητα με το \[(1)\] αλλά αντίθετο φορτίο εισέρχεται στο ίδιο φίλτρο ταχυτήτων. Ποια απ’ τις παρακάτω προτάσεις είναι σωστή; 10. Ποια απ’ τις παρακάτω προτάσεις είναι σωστή; Βόρειο και νότιο μαγνητικό πόλο μπορούμε να παρατηρήσουμε στο μαγνητικό πεδίο: 11. Αρνητικά φορτισμένο σωματίδιο εισέρχεται από σημείο Κ σε ομογενές μαγνητικό πεδίο με ορμή \[\vec{p}\] και ταχύτητα \[ υ_1 \] που είναι κάθετη στις δυναμικές γραμμές του πεδίου και στο όριό του ΔΕ όπως φαίνεται στο παρακάτω σχήμα. Το σωματίδιο δέχεται μόνο τη δύναμη απ’ το πεδίο και εξέρχεται από σημείο Λ του ίδιου ορίου ΔΕ εκτελώντας κυκλική κίνηση ακτίνας \[R_1\] και συχνότητας \[f_1\]. Λόγω της παραμονής του στο πεδίο η μεταβολή του μέτρου της ορμής του είναι \[ Δ | \vec{ p } | \] ενώ το μέτρο της μεταβολής της ορμής του είναι \[ | Δ \vec{p} | \]. Ποιες απ’ τις παρακάτω προτάσεις είναι σωστές;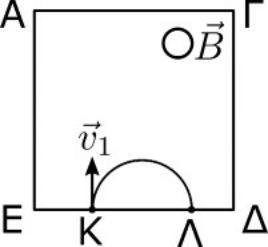
14. Ποιες απ’ τις επόμενες προτάσεις είναι σωστές; Για να βρούμε την ένταση του μαγνητικού πεδίου \[\vec{Β}\] ενός ρευματοφόρου αγωγού σ’ ένα σημείο Α του μαγνητικού του πεδίου χωρίζουμε ολόκληρο τον αγωγό σε στοιχειώδη τμήματα \[Δ\ell_1\, , \, Δ\ell_2\, , … \] και τότε: 18. Ποια απ’ τις παρακάτω προτάσεις είναι σωστή; Στο νόμο του Ampere \[∑B\cdot Δ\ell\cdot συνθ=μ_0 Ι_{εγκ}\], το \[Ι_{εγκ}\] είναι: 19. Ο αγωγός ΚΛ του παρακάτω σχήματος α αποτελείται από δύο πανομοιότυπους ευθύγραμμους αγωγούς ΚΟ και ΟΛ που έχουν συγκολληθεί κάθετα στο κοινό τους άκρο Ο. Ο κάθε αγωγός έχει μήκος \[\ell\]. Ο αγωγός ΚΟΛ διαρρέεται από ρεύμα έντασης \[Ι\] και αρχικά είναι τοποθετημένος όπως στο σχήμα 1 μέσα σε ομογενές μαγνητικό πεδίο έντασης μέτρου \[B\]. Η δύναμη Laplace που δέχεται ο αγωγός ΚΟΛ έχει μέτρο \[F_1\].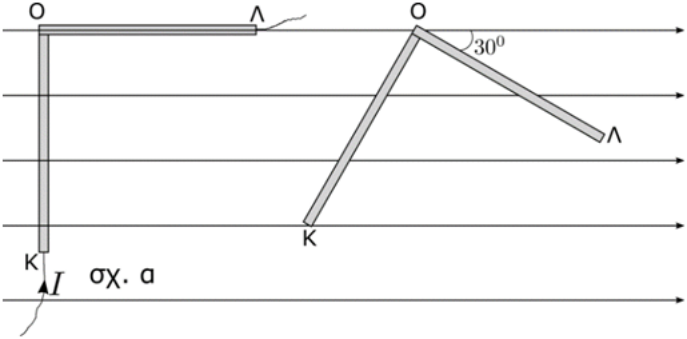
Α) Αν στρέψω τον αγωγό ΚΟΛ κατά \[90^0\] ως προς άξονα κάθετο στο επίπεδό του που διέρχεται απ’ το σημείο Ο, τότε αυτός θα δέχεται δύναμη Laplace μέτρου \[F_2\] με:
α) \[F_2=F_1\], β) \[F_2=\frac{F_1}{2}\], γ) \[F_2=2F_1\].
B) Αν στρέψω τον αγωγό κατά γωνία \[30^0\] ως προς τον ίδιο άξονα περιστροφής, τότε αυτός θα δέχεται δύναμη Laplace μέτρου \[F_3\] με:
α) \[F_3=\frac{ \sqrt{3}-1 }{2} F_1 \], β) \[F_3=\frac{F_1}{2}\], γ) \[F_3=2F_1\].
23. Ο αγωγός του παρακάτω σχήματος είναι τμήμα κύκλου ακτίνας \[r\] και κέντρου Κ. Η επίκεντρη γωνία που του αντιστοιχεί είναι \[Δθ\] μετρημένη σε \[rad\]. Ο αγωγός διαρρέεται από ρεύμα έντασης \[Ι\] που η φορά του φαίνεται στο σχήμα. Αν \[μ_0\] η μαγνητική διαπερατότητα του κενού, τότε η ένταση του μαγνητικού πεδίου του αγωγού στο κέντρο του Κ: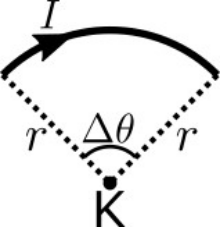
24. Σωματίδιο μάζας \[m\] και φορτίου \[q\] εισέρχεται μέσα σε ομογενές μαγνητικό πεδίο έντασης \[\vec{B}\] με ταχύτητα \[\vec{υ}\] που σχηματίζει γωνία \[φ\] \[(0 < φ < 90^0)\] με τις δυναμικές του γραμμές. Ποιες απ’ τις παρακάτω προτάσεις είναι σωστές; Αν μεταβάλω τη γωνία \[φ\] κατά την είσοδο του σωματιδίου στο πεδίο αλλά αυτή να παραμένει συνεχώς μεταξύ των τιμών \[0 < φ < 90^0 \] τότε δεν θα μεταβληθεί: 25. Στον επιλογέα ταχυτήτων του παρακάτω σχήματος το μαγνητικό του πεδίο έχει ένταση \[\vec{B}\] και το ηλεκτρικό πεδίο έχει ένταση \[\vec{Ε}\]. Δέσμη πρωτονίων (μάζας \[m_p\] και φορτίου \[q_p=e\]) εισέρχεται σε επιλογέα ταχυτήτων με ταχύτητα \[υ\] κάθετη στις δυναμικές γραμμές των δύο πεδίων του. Η δέσμη δεν αποκλίνει κατά το πέρασμά της μέσα απ’ τον επιλογέα. Οι βαρυτικές δυνάμεις και οι ηλεκτροστατικές αλληλεπιδράσεις μεταξύ των σωματιδίων της δέσμης θεωρούνται αμελητέες. Αν αντί για δέσμη πρωτονίων είχαμε δέσμη σωματιδίων \[α\] (μάζας \[m_α=4m_p\] και \[q_α=2e\]) τότε: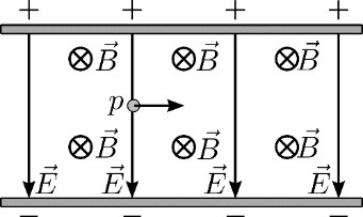
26. Ποιες από τις παρακάτω προτάσεις είναι σωστές; Το διάνυσμα της έντασης του μαγνητικού πεδίου στο κέντρο κυκλικού ρευματοφόρου αγωγού: 27. Οι δύο κατακόρυφοι αγωγοί του παρακάτω σχήματος είναι απείρου μήκους και διαρρέονται από ρεύματα εντάσεων \[Ι_1,\, Ι_2\]. Τρίτος αγωγός (3) είναι κυκλικός, εφάπτεται στους άλλους δύο με μονωτικές επαφές και έχει το επίπεδό του κάθετο σ’ αυτούς. Ο αγωγός (3) έχει ακτίνα \[α\] και διαρρέεται από ρεύμα έντασης \[Ι_3\]. Στο κέντρο Κ του αγωγού (3) η ένταση του συνολικού πεδίου λόγω των τριών αγωγών είναι διάνυσμα παράλληλο των δύο αγωγών και έχει μέτρο \[Β_Κ=μ_0 \frac{ Ι_1 }{α}\]. Για τους αγωγούς ισχύει: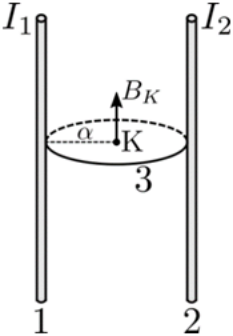
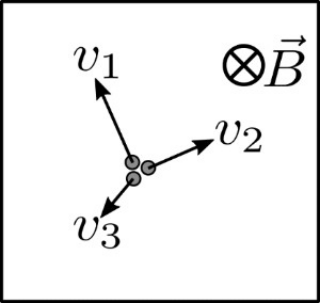
28. Ποια απ’ τις παρακάτω προτάσεις είναι σωστή; Η μάζα \[m\] του ηλεκτρονίου: 29. Σε χώρο που αμελούνται οι βαρυτικές δυνάμεις ένα σωματίδιο κινείται ευθύγραμμα και ομαλά. Ποιες απ’ τις παρακάτω προτάσεις είναι σωστές; 30. Τρία διαφορετικά αρνητικά ιόντα βάλλονται ταυτόχρονα την \[t=0\] μέσα σε ομογενές μαγνητικό πεδίο με ταχύτητες μέτρων \[ υ_1 > υ_2 > υ_3\] αντίστοιχα που είναι κάθετες στις δυναμικές γραμμές του πεδίου όπως φαίνεται στο παρακάτω σχήμα. Τα ιόντα αφού διαγράψουν από έναν πλήρη κύκλο ακτίνων \[ R_1\, , \, R_2 \, , \, R_3\] αντίστοιχα, επιστρέφουν για πρώτη φορά στο σημείο βολής τους την ίδια χρονική στιγμή επιδρώντας σ’ αυτά μόνο οι δυνάμεις που δέχονται απ’ το μαγνητικό πεδίο. Τα μέτρα των δυνάμεων Lorentz F_Lo που δέχονται τα ιόντα απ’ το πεδίο ισχύει: