4. Τροχός στρέφεται γύρω από σταθερό οριζόντιο άξονα εκτελώντας ομαλά μεταβαλλόμενη κίνηση κατά τη φορά των δεικτών του ρολογιού. Ο άξονας περιστροφής είναι κάθετος στις βάσεις του και διέρχεται απ’ τα κέντρα τους. Ποιες από τις παρακάτω προτάσεις είναι σωστές;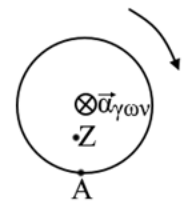
7. Ο τροχός του παρακάτω σχήματος στρέφεται κατά τη φορά των δεικτών του ρολογιού γύρω από οριζόντιο άξονα που είναι κάθετος στις βάσεις του και διέρχεται απ’ τα κέντρα τους. Η στροφική κίνηση είναι ομαλά μεταβαλλόμενη και το μέτρο της γωνιακής της ταχύτητας συνεχώς μειώνεται. Ποιες από τις παρακάτω προτάσεις είναι σωστές;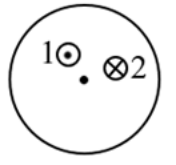
8. Για να ισορροπεί ένα αρχικά ακίνητο στερεό σώμα στο οποίο ασκούνται πολλές ομοεπίπεδες δυνάμεις πρέπει να ισχύουν οι σχέσεις: 11. Το παρακάτω στερεό (σχ. α) είναι ένα καρούλι. Αυτό αποτελείται από έναν ομογενή κύλινδρο που στα άκρα του έχουμε κολλήσει δύο όμοιους ομογενείς δίσκους έτσι ώστε τα κέντρα τους να βρίσκονται πάνω στον άξονα του κυλίνδρου. Η ακτίνα του κυλίνδρου είναι \[r\] ενώ του κάθε δίσκου είναι \[R\]. Τοποθετούμε το καρούλι πάνω σε δύο οριζόντιους υπερυψωμένους δοκούς ώστε η περιφέρεια του κυλίνδρου να ακουμπά σ’ αυτούς ενώ οι περιφέρειες των δίσκων βρίσκονται στον αέρα χωρίς ν’ ακουμπούν ούτε στις δοκούς ούτε στο έδαφος. Στο σχήμα β φαίνεται πρόσοψη του καρουλιού. Το καρούλι αρχίζει να κινείται και ο κύλινδρος εκτελεί Κ.Χ.Ο. με σταθερή γωνιακή ταχύτητα μέτρου \[ω\] και ταχύτητα κέντρου μάζας μέτρου \[υ_{cm}\].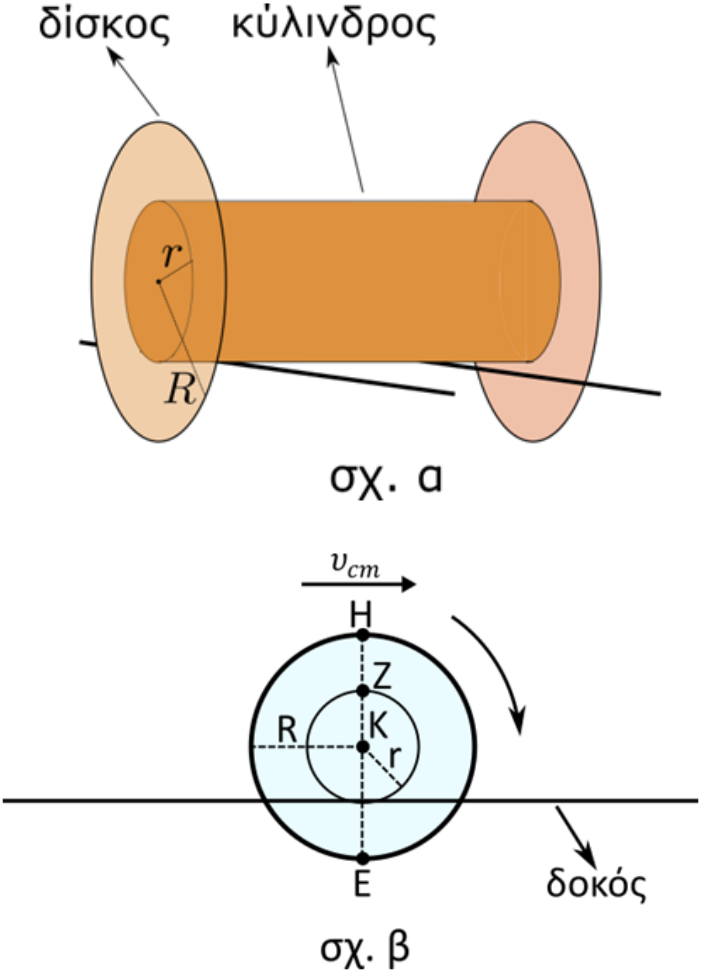
A) Το μέτρο της ταχύτητας του κέντρου μάζας του δίσκου είναι:
α) \[ωR\], β) \[ωr\], γ) \[ω(R-r)\].
Β) Το ανώτερο σημείο Ζ της περιφέρειας του κυλίνδρου έχει ταχύτητα μέτρου:
α) \[υ_{cm}\], β) \[\frac{3}{2} υ_{cm}\], γ) \[2υ_{cm}\].
Γ) Το ανώτερο σημείο Η του ενός δίσκου έχει ταχύτητα μέτρου:
α) \[υ_{cm} \left( \frac{R}{r} + 1 \right)\], β) \[ υ_{cm} \left(\frac{R}{r}-1 \right)\], γ) \[2υ_{cm}\].
Δ) Το κατώτερο σημείο Ε του ενός δίσκου έχει ταχύτητα μέτρου:
α) \[υ_{cm} \left( \frac{R}{r}-1 \right)\] και φορά προς τ’ αριστερά.
β) \[ υ_{cm} \left( \frac{R}{r}-1 \right)\] και φορά προς τα δεξιά.
γ) μηδέν.
12. Ένα στερεό σώμα που αρχικά είναι ακίνητο έχει τη δυνατότητα να περιστρέφεται γύρω από το σταθερό (ακλόνητο) κατακόρυφο άξονα \[z’z\]. Στο στερεό ασκείται οριζόντια δύναμη \[\vec{F}\] που απέχει απόσταση \[R\] από τον άξονα \[z'z\], όπως φαίνεται στο σχήμα.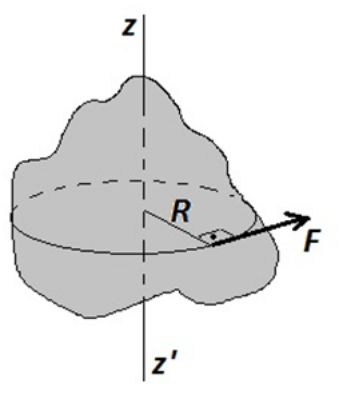
16. Ομογενής λεπτή ράβδος ΟΑ εκτελεί στροφική κίνηση πάνω σε οριζόντιο επίπεδο και γύρω από σταθερό κατακόρυφο άξονα που διέρχεται απ’ το κέντρο της. Στο παρακάτω σχήμα φαίνεται η μεταβολή της γωνιακής της ταχύτητας με το χρόνο. Ποιες από τις παρακάτω προτάσεις είναι σωστές;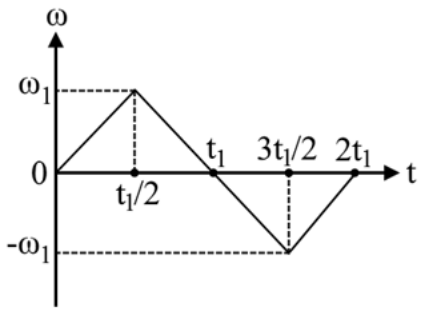
17. Ομογενής τροχός ακτίνας \[R\] κυλίεται χωρίς να ολισθαίνει κατεβαίνοντας σε κεκλιμένο επίπεδο με σταθερή επιτάχυνση μέτρου \[α_{cm}\] και σταθερή γωνιακή επιτάχυνση μέτρου \[α_{γων}\]. Ποια απ’ τις επόμενες προτάσεις είναι σωστή; 20. Σφαίρα εκτελεί στροφική κίνηση γύρω από κατακόρυφο άξονα περιστροφής που ταυτίζεται με μια διάμετρό της. Στο παρακάτω σχήμα φαίνεται το διάγραμμα της γωνιακής της ταχύτητας με το χρόνο. Ποιες από τις παρακάτω προτάσεις είναι σωστές;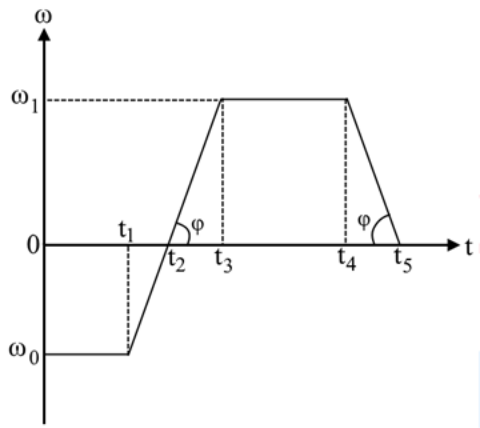
21. Ο ομογενής τροχός ακτίνας \[R\] του παρακάτω σχήματος στρέφεται δεξιόστροφα με σταθερή γωνιακή ταχύτητα και ταυτόχρονα μεταφέρεται προς τα δεξιά με σταθερή ταχύτητα μέτρου \[υ_{cm}\]. Το σημείο επαφής του τροχού με το έδαφος έχει κάθε στιγμή ταχύτητα μέτρου \[υ_Α=\frac{ υ_{cm} }{2}\] και φορά προς τ’ αριστερά.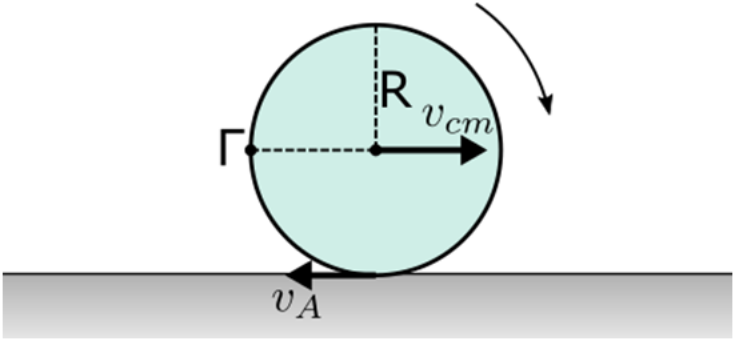
Α) Αν σε χρόνο \[Δt\] ένα σημείο της περιφέρειας του τροχού διαγράφει μήκος τόξου \[Δs\] και στον ίδιο χρόνο το κέντρο μάζας του μεταφέρεται κατά \[Δx_{cm}\] τότε το πηλίκο \[\frac{ Δs }{ Δx_{cm} } \] είναι:
α) \[\frac{3}{2}\], β) \[\frac{2}{3}\], γ) \[1\], δ) \[2\].
Β) Το μέτρο της ταχύτητας του σημείου Γ της περιφέρειάς που απέχει \[R\] απ’ το έδαφος έχει ταχύτητα:
α) \[ \sqrt{2} υ_{cm} \], β) \[\frac{ \sqrt{13} }{ 2 } υ_{cm}\], γ) \[ \frac{ \sqrt{5} }{2} υ_{cm}\].
29. Να επιλέξετε τις σωστές από τις προτάσεις που ακολουθούν. Δίνονται τρεις ομοεπίπεδες δυνάμεις \[\vec{F}_1,\, \vec{F}_2\] και \[\vec{F}_3\], οι οποίες έχουν ίσα μέτρα και ένα σημείο Ο του επιπέδου τους. Οι αποστάσεις (ΟΑ), (ΟΒ) και (ΟΓ) είναι ίσες μεταξύ τους.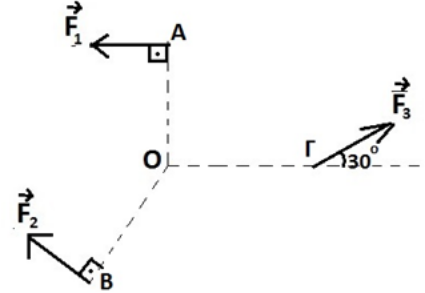
30. Δύο στερεά σώματα (1) και (2) στρέφονται γύρω από σταθερούς άξονες και οι γραφικές παραστάσεις των γωνιακών τους ταχυτήτων με το χρόνο φαίνονται στα παρακάτω διαγράμματα στο ίδιο σύστημα αξόνων.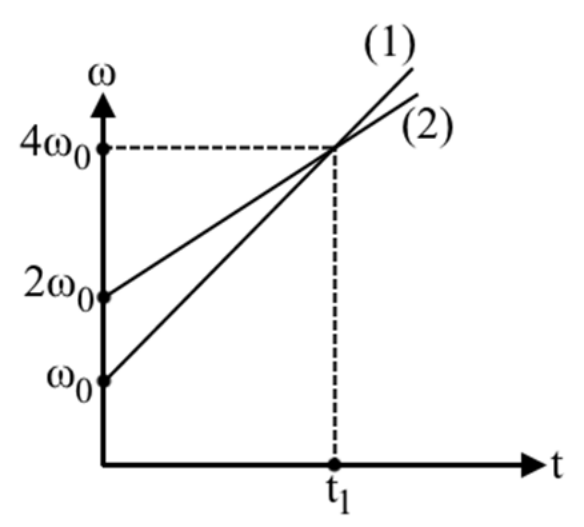
Α) Για τις γωνιακές επιταχύνσεις \[α_{γων_1 },\, α_{γων_2 }\] των δύο στερεών ισχύει: α) \[α_{γων_1}=α_{γων_2 }\], β) \[α_{γων_1 }=1,5α_{γων_2}\],
γ) \[α_{γων_1 }=2α_{γων_2 }\], δ) \[α_{γων_2 }=1,5α_{γων_1 }\].
Β) Η χρονική στιγμή \[t_2\] μέχρι την οποία τα δύο στερεά έχουν στραφεί κατά ίσες γωνίες απ’ τη στιγμή \[t_0=0\] είναι:
α) \[2t_1\], β) \[1,5t_1\], γ) \[4t_1\].
