3. Τα σώματα του παρακάτω σχήματος έχουν μάζες \[m_1=m\] και \[m_2=2m\] και ηρεμούν προσδεμένα στα άκρα πανομοιότυπων ιδανικών ελατηρίων πάνω σε λείο οριζόντιο δάπεδο. Την \[t=0\] προσδίνω στα σώματα \[Σ_1\, ,\, Σ_2\] ταχύτητες μέτρου \[υ_0\] και \[υ_0\sqrt{2} \] αντίστοιχα κατά τη διεύθυνση των αξόνων των ελατηρίων. Η ταχύτητα του \[Σ_1\] έχει φορά προς τα δεξιά και του \[Σ_2\] προς τ’ αριστερά.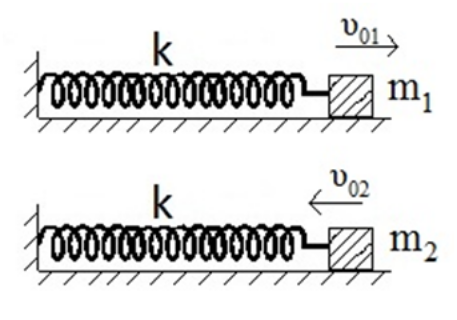
Α. Ο λόγος των μέγιστων επιταχύνσεων των δύο σωμάτων είναι:
α. \[\frac{α_{max,1}}{α_{max,2}} =1\].
β. \[ \frac{ α_{max,1}} {α_{max,2}} =2\].
γ. \[\frac { α_{max,1} }{ α_{max,2} } =\sqrt{2}\].
δ. \[\frac{ α_{max,1} }{ α_{max,2} } =\frac{\sqrt{2} }{2}\].
Β. Οι αρχικές φάσεις των δύο α.α.τ. μπορεί να είναι:
α. \[φ_{0,1}=π\] και \[φ_{0,2}=π\].
β. \[φ_{0,1}=π\] και \[φ_{0,2}=0\].
γ. \[φ_{0,1}=π\] και \[φ_{0,2}=\frac{π}{2}\].
δ. \[φ_{0,1}=π\] και \[φ_{0,2}=\frac{3π}{2}\]. Γ. Ο λόγος των μέγιστων δυναμικών ενεργειών των δύο ταλαντωτών είναι:
α. \[ \frac{U_{T,max,1}}{U_{T,max,2}} =1\].
β. \[ \frac{ U_{T,max,1}}{U_{T,max,2}} =\frac{1}{4}\].
γ. \[ \frac{ U_{T,max,1} }{ U_{T,max,2} }=2.\].
δ. \[ \frac{U_{T,max,1}} { U_{T,max,2} } =\frac{\sqrt{2}}{2}\].
4. Στη θέση ισορροπίας μιας α.α.τ.: 6. Ένας απλός αρμονικός ταλαντωτής εκτελεί ταλάντωση γύρω απ’ τη Θ.Ι. του Ο μεταξύ των σημείων Κ και Λ με περίοδο \[Τ\]. Τη στιγμή \[t_1\] ο ταλαντωτής βρίσκεται στο σημείο Ζ της τροχιάς του και κινείται προς τα δεξιά. Τη χρονική στιγμή \[t_1+T\] ο ταλαντωτής: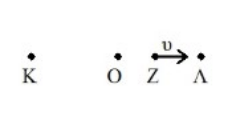
7. Στο παρακάτω σχήμα φαίνεται η μεταβολή της επιτάχυνσης ενός απλού αρμονικού ταλαντωτή σε συνάρτηση με την απομάκρυνση \[x\]. Σε μια περίοδο ο ταλαντωτής διανύει διάστημα \[0,4\, m\].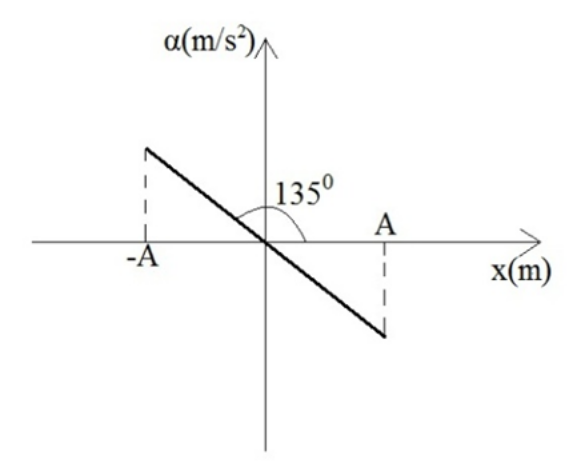
Α. Το χρονικό διάστημα μεταξύ δύο διαδοχικών μηδενισμών της ταχύτητας του ταλαντωτή είναι:
α. \[0,5\, sec\].
β. \[1\, sec\].
γ. \[π\, sec\].
δ. \[\frac{π}{2}\, sec\].
Β. Η μέγιστη επιτάχυνση του ταλαντωτή είναι:
α. \[0,1 \frac{m}{s^2}\]
β. \[ 0,2 \frac{m}{s^2} \]
γ. \[ 0,4 \frac{m}{s^2} \]
δ. \[ 1 \frac{m}{s^2} \]
14. Δύο σώματα με ίσες μάζες είναι δεμένα και ισορροπούν στα πάνω ελεύθερα άκρα δύο ιδανικών ελατηρίων που έχουν ίδιο φυσικό μήκος που τα κάτω άκρα τους είναι προσδεμένα σε οριζόντιο δάπεδο. Εκτρέπω και τα δύο σώματα κατά \[d\] κατακόρυφα προς τα κάτω και απ’ τις θέσεις αυτές τα αφήνω ελεύθερα. Τα σώματα εκτελούν α.α.τ. Τα ελατήρια έχουν σταθερές \[k_1\], \[k_2\] με \[k_1>k_2\]. 17. Ποιες από τις παρακάτω προτάσεις είναι σωστές; Σε μια α.α.τ.: 19. Ένας απλός αρμονικός ταλαντωτής εκτελεί ταλάντωση γύρω απ’ τη Θ.Ι. του Ο μεταξύ των σημείων Κ και Λ με περίοδο \[Τ\]. Τη στιγμή \[t_1\] ο ταλαντωτής βρίσκεται στο σημείο Ζ της τροχιάς και έχει ταχύτητα προς τα δεξιά. Τη χρονική στιγμή \[t_1+T\] ο ταλαντωτής: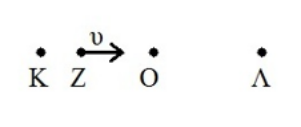
20. Σε μια α.α.τ. τη στιγμή \[t_1\] ο ταλαντωτής έχει απομάκρυνση \[x=x_1>0\]. Αυτό σημαίνει ότι την \[t_1\] 23. Ποιες από τις παρακάτω προτάσεις είναι σωστές; Σε μια α.α.τ.: 25. Σε μια α.α.τ. η κινητική ενέργεια του ταλαντωτή σε σχέση με την απομάκρυνσή του δίνεται απ’ τη σχέση \[Κ=4,5-50x^2\] (S.I.). Ο ταλαντωτής έχει μάζα \[1\, kg\].A. Το πλάτος του ταλαντωτή είναι:
α. \[A=0,1\, m\]. β. \[A=0,2\, m\]. γ. \[A=0,3\, m\]. δ. \[A=0,4\, m\].
Β. Ο χρόνος μεταξύ δύο διαδοχικών περασμάτων του ταλαντωτή απ’ τη Θ.Ι. του είναι:
α. \[Δt=0,05π\, sec\]. β. \[Δt=0,1π\, sec\]. γ. \[Δt=0,15π\, sec\]. δ. \[Δt=0,2π\, sec\].
26. Σώμα εκτελεί α.α.τ. και η δύναμη επαναφοράς του σώματος δίνεται απ’ τη σχέση \[ΣF=-200⋅x\] (S.I.). Αν η ενέργεια της α.α.τ. είναι \[Ε_Τ=1 J\], τότε στη διάρκεια μιας περιόδου:Α. ο ταλαντωτής διανύει απόσταση:
α. \[0,1\, m\]. β. \[0,2\, m\]. γ. \[0,3\, m\]. δ. \[0,4 \, m\].
B. ο ταλαντωτής μετατοπίζεται κατά:
α. \[0\, m\]. β. \[0,1\, m\]. γ. \[0,4\, m\]. δ. \[-0,4\, m\].
28. Υλικό σημείο εκτελεί α.α.τ. πλάτους \[Α\]. 30. Σώμα εκτελεί α.α.τ. Στο παρακάτω σχήμα φαίνεται το διάγραμμα της μεταβολής της απομάκρυνσης του ταλαντωτή σε συνάρτηση με το χρόνο. Ποιες από τις επόμενες προτάσεις είναι σωστές;