2. Σύστημα ιδανικό ελατήριο-σώμα βρίσκεται σε λείο οριζόντιο επίπεδο και ισορροπεί ακίνητο στη θέση που το ελατήριο έχει το φυσικό του μήκος. Εκτρέπω το σώμα απ’ τη Θ.Ι. του κατά \[x_0\] στη διεύθυνση του άξονα του ελατηρίου και την \[t=0\] το αφήνω ελεύθερο να κινηθεί. Το σύστημα εκτελεί α.α.τ. Ποιες απ’ τις παρακάτω προτάσεις είναι σωστές; 4. Στο παρακάτω διάγραμμα φαίνονται οι γραφικές παραστάσεις της μεταβολής των φάσεων σε συνάρτηση με το χρόνο για δύο απλούς αρμονικούς ταλαντωτές. Ποιες από τις παρακάτω προτάσεις είναι σωστές;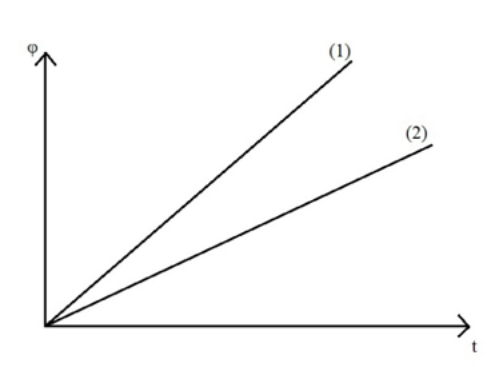
8. Ταλαντωτής εκτελεί φθίνουσα ταλάντωση με αρχικό πλάτος \[Α_0\] που η αντιτιθέμενη δύναμη στην κίνησή του είναι της μορφής \[F_{αν}=-bυ\] όπου \[b\] η σταθερά απόσβεσης. Αν ο ίδιος ταλαντωτής εκτελούσε ίδιας μορφής ταλάντωση με ίδιο αρχικό πλάτος αλλά με μεγαλύτερη σταθερά απόσβεσης τότε: 10. Σε μια φθίνουσα μηχανική ταλάντωση που η δύναμη αντίστασης στην κίνηση συνδέεται με την ταχύτητα του ταλαντωτή σύμφωνα με τη σχέση \[F_{αν}=-bυ\], η περίοδος της φθίνουσας ταλάντωσης: 11. Υλικό σημείο εκτελεί α.α.τ. πλάτους \[Α\] και ενέργειας \[Ε_Τ\]. Στο παρακάτω διάγραμμα φαίνεται η δυναμική ενέργεια \[U_T\] και η κινητική ενέργεια \[Κ\] της α.α.τ. σε συνάρτηση με την απομάκρυνση του σημείου απ’ τη Θ.Ι. του. Ποιες από τις παρακάτω προτάσεις είναι σωστές;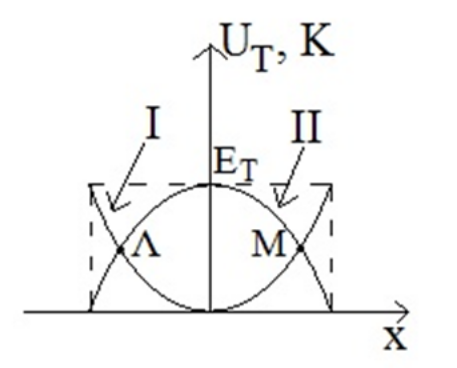
12. Σύστημα ιδανικό ελατήριο-σώμα εκτελεί εξαναγκασμένη μηχανική ταλάντωση με τη βοήθεια διεγέρτη-τροχού. Ποιες από τις παρακάτω προτάσεις είναι σωστές; Όταν μεταβάλλω τη συχνότητα του διεγέρτη μεταβάλλεται: 15. Ποιες από τις παρακάτω προτάσεις που αφορούν την α.α.τ. είναι σωστές; 19. Τα σώματα \[Σ_1\], \[Σ_2\] ισορροπούν στα πάνω άκρα κατακόρυφων ιδανικών ελατηρίων σταθεράς \[k_1\, ,\, k_2\] που τα άλλα άκρα τους είναι στερεωμένα σε οριζόντιο δάπεδο. Τα σώματα έχουν ίσες μάζες. Εκτοξεύω τα δύο σώματα απ’ τις Θ.Ι. τους με κατακόρυφες ταχύτητες μέτρων \[υ_1\] και \[υ_2=\frac{υ_1}{2}\] αντίστοιχα και αυτά αρχίζουν να εκτελούν α.α.τ. Παρατηρώ ότι τη στιγμή που το \[Σ_1\] επιστρέφει στη Θ.Ι. του για 1η φορά μετά την εκτόξευση του, το \[Σ_2\] ακινητοποιείται για πρώτη φορά.Α. Για τις σταθερές των ελατηρίων \[k_1\, ,\, k_2\] ισχύει:
α. \[k_1=k_2 \sqrt{2}\].
β. \[k_1=4k_2\].
γ. \[k_1=\frac{k_2}{4}\].
δ. \[k_1=\frac{k_2}{ \sqrt{2} }\].
Β. Για τις μέγιστες επιταχύνσεις των σωμάτων \[α_{max,1}\, ,\, α_{max,2}\] ισχύει:
α. \[α_{max,1}=α_{max,2}\].
β. \[α_{max,1}=2α_{max,2}\].
γ. \[α_{max,1}=4α_{max,2}\].
δ. \[α_{max,1}=\sqrt{2} α_{max,2}\].
20. Στο παρακάτω διάγραμμα φαίνεται η μεταβολή της κινητικής ενέργειας του ταλαντωτή σε συνάρτηση με το χρόνο. Ποιες από τις επόμενες προτάσεις είναι σωστές;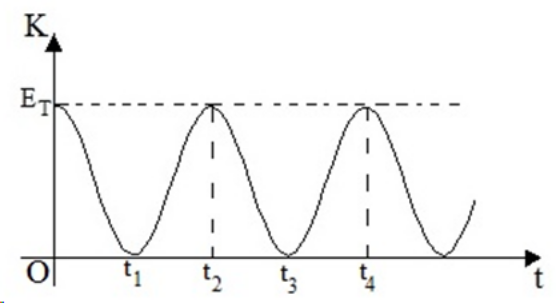
23. Σώμα εκτελεί α.α.τ. Στο παρακάτω σχήμα φαίνεται το διάγραμμα της μεταβολής της επιτάχυνσης του ταλαντωτή σε συνάρτηση με το χρόνο. Ποιες από τις επόμενες προτάσεις είναι σωστές;
24. Ποιες απ’ τις παρακάτω προτάσεις είναι σωστές; Σε μια α.α.τ.: 25. Στο παρακάτω διάγραμμα φαίνεται η μεταβολή της επιτάχυνσης του ταλαντωτή σε συνάρτηση με την απομάκρυνσή του απ’ τη Θ.Ι. του. Ποιες από τις παρακάτω προτάσεις είναι σωστές;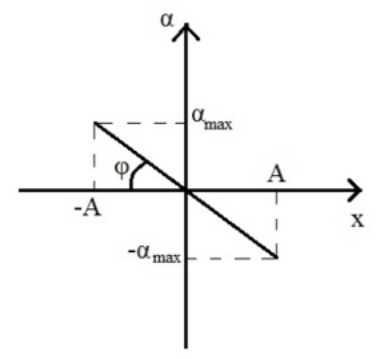
27. Στο παρακάτω διάγραμμα φαίνεται η μεταβολή της δυναμικής ενέργειας του ταλαντωτή σε συνάρτηση με το χρόνο. Ποιες από τις επόμενες προτάσεις είναι σωστές;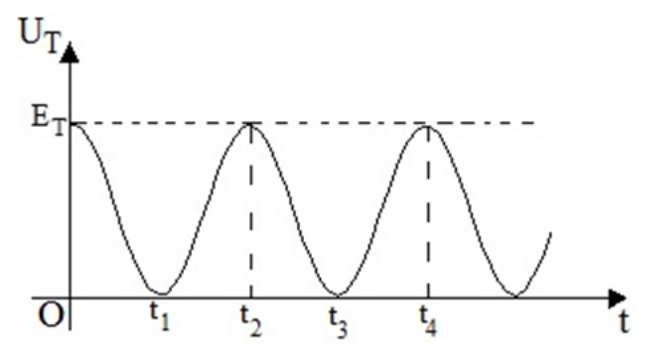
29. Ένα κρυστάλλινο ποτήρι μπορεί να σπάσει λόγω ενός ηχητικού κύματος όταν: 30. Υλικό σημείο εκτελεί α.α.τ. μεταξύ των ακραίων θέσεων Κ, Λ γύρω απ’ τη θέση ισορροπίας Ο. Ποιες από τις παρακάτω προτάσεις είναι σωστές; Το έργο της δύναμης επαναφοράς:
