1. Σε ελαστική ομογενή χορδή που ταυτίζεται με τον ημιάξονα \[Οx\] διαδίδεται εγκάρσιο αρμονικό κύμα χωρίς αρχική φάση. Στο παρακάτω διάγραμμα φαίνεται το διάγραμμα της φάσης των σημείων του μέσου σε συνάρτηση με την απόστασή τους απ’ την αρχή του άξονα τη χρονική στιγμή \[t_1=4\, s\]. Ποιες από τις παρακάτω προτάσεις είναι σωστές;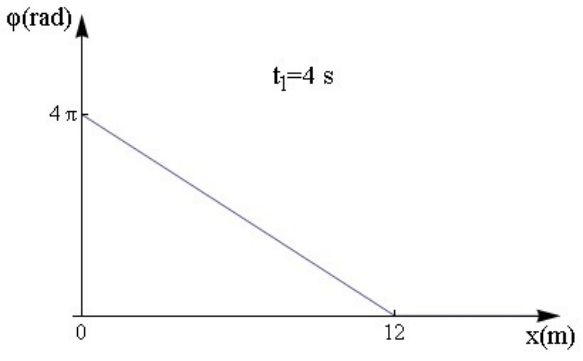
2. Στο παρακάτω σχήμα φαίνεται το στιγμιότυπο τη στιγμή \[t_1\] εγκάρσιου αρμονικού κύματος που διαδίδεται κατά τη διεύθυνση του άξονα \[x' x\]. Το κύμα περιγράφεται απ’ την εξίσωση \[y=A ημ2π\left( \frac{t}{T} - \frac{ x }{ λ } \right) \]. Ποιες από τις παρακάτω προτάσεις είναι σωστές;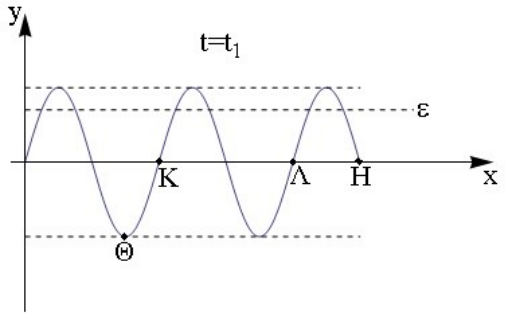
3. Αρμονικό κύμα διαδίδεται κατά τη διεύθυνση του άξονα \[x' Ox\] και έχει εξίσωση της μορφής \[y=A ημ2π\left(\frac{t}{T}+\frac{x}{λ}\right)\]. Στο παρακάτω σχήμα φαίνεται το στιγμιότυπο του κύματος τη στιγμή \[t_1\]. Ποιες από τις παρακάτω προτάσεις είναι σωστές;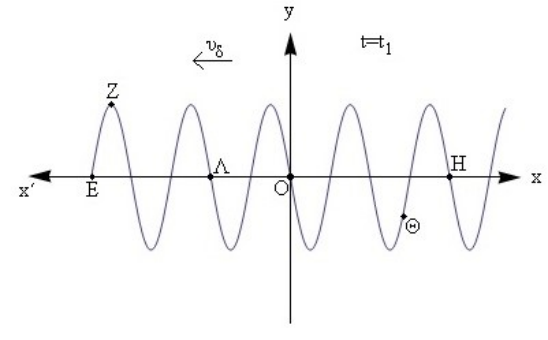
5. Σε επιφάνεια υγρού δύο σύγχρονες πηγές \[Π_1\, , \, Π_2\] δημιουργούν εγκάρσια αρμονικά κύματα ίδιου πλάτους \[Α\] και ταχύτητας διάδοσης \[υ_δ=5\, \frac{ m }{ s } \]. Σημείο Λ της επιφάνειας απέχει αποστάσεις \[r_1=1\, m\] και \[r_2=0,5\, m\]. Για να εμφανίζεται στο Λ ενισχυτική συμβολή η συχνότητα των πηγών πρέπει να παίρνει τις τιμές: 7. Δύο σύγχρονες πηγές \[Π_1\, ,\, Π_2\] δημιουργούν στην επιφάνεια υγρού εγκάρσια αρμονικά κύματα ίδιου πλάτους \[Α\] και μήκους κύματος \[λ\]. Το σημείο Ζ απέχει απ’ τις δύο πηγές αποστάσεις \[r_{1Z}=6\, λ\] και \[r_{2Z}=2\, λ\]. Μειώνω αργά τις συχνότητες των δύο πηγών ώστε να παραμένουν συνεχώς σύγχρονες. Το σημείο Ζ στη διάρκεια της μείωσης των συχνοτήτων: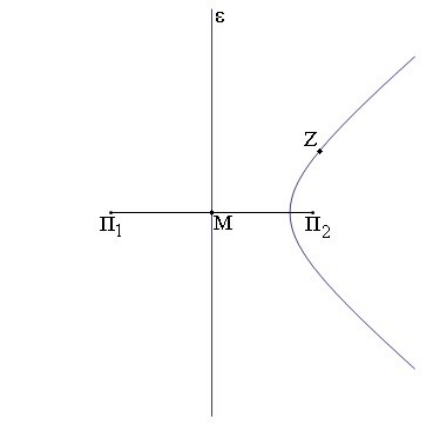
9. Δύο σύγχρονες πηγές \[Π_1\, ,\, Π_2 \] δημιουργούν στην επιφάνεια υγρού εγκάρσια αρμονικά κύματα ίδιου πλάτους \[Α\], μήκους κύματος \[λ\], περιόδου \[Τ\] και \[φ_0=0\]. Στο παρακάτω σχήμα φαίνεται η μεταβολή του πλάτους του σημείου Λ της επιφάνειας υγρού με το χρόνο. Ποιες από τις παρακάτω προτάσεις είναι σωστές;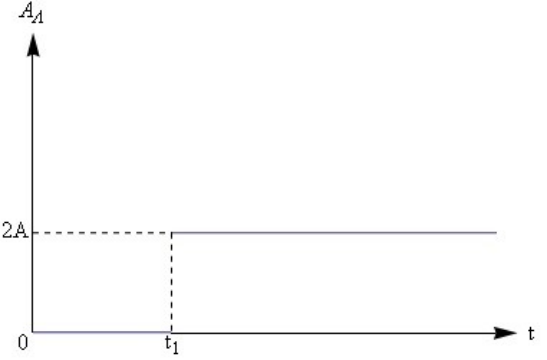
10. Δύο σύγχρονες πηγές \[Π_1\, , \, Π_2\] δημιουργούν στην επιφάνεια υγρού εγκάρσια αρμονικά κύματα ίδιου πλάτους \[Α\], ταχύτητας διάδοσης \[υ_δ\] και έχουν εξισώσεις ταλάντωσης της μορφής \[y=A ημ \frac{ 2πt}{T}\]. Σημείο Ζ της επιφάνειας απέχει απ’ τις δύο πηγές αποστάσεις \[r_{1Z}\, , \, r_{2Z}\] με \[r_{1Z} < r_{2Z} \]. Το σημείο Ζ αρχίζει να ταλαντώνεται όταν η πηγή \[Π_2\] περνά για έκτη φορά απ’ τη Θ.Ι. της μετά την έναρξη της ταλάντωσής της. Στο παρακάτω σχήμα φαίνεται η χρονική μεταβολή της ταχύτητας του Ζ. Αν υποδιπλασιάσουμε τη συχνότητα ταλάντωσης των δύο πηγών ώστε αυτές να παραμένουν σύγχρονες και να ταλαντώνονται με ίδιο πλάτος \[Α\], τότε το σημείο Ζ: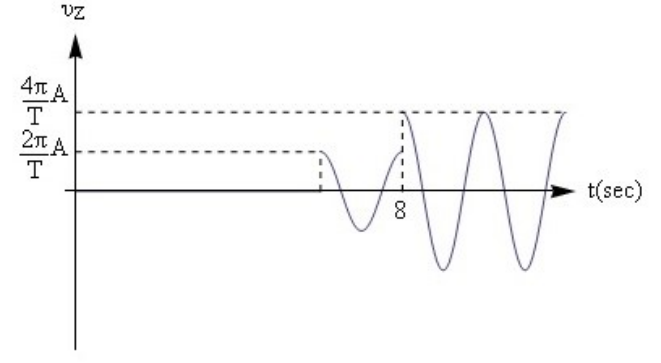
13. Δύο σύγχρονες πηγές \[Π_1\, ,\, Π_2\] δημιουργούν στην επιφάνεια υγρού εγκάρσια αρμονικά κύματα ίδιου πλάτους \[Α\] και μήκους κύματος \[λ\]. Το σημείο Η απέχει από τις δύο πηγές \[r_{1H}=2\,λ\] και \[r_{2H}=5\, λ\] αντίστοιχα. Αυξάνω αργά τη συχνότητα των δύο πηγών ώστε αυτές να παραμένουν συνεχώς σύγχρονες. Το σημείο H στη διάρκεια της αύξησης των δύο συχνοτήτων: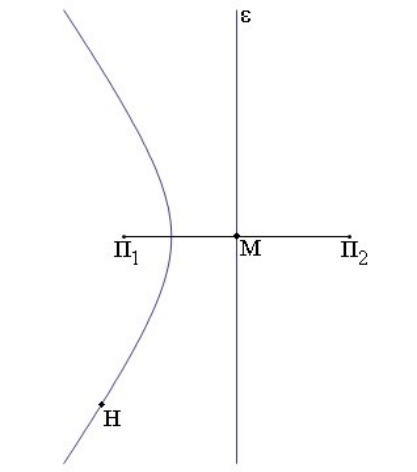
14. Δύο σύγχρονες πηγές \[Π_1\, ,\, Π_2\] δημιουργούν στην επιφάνεια υγρού εγκάρσια αρμονικά κύματα ίδιου πλάτους \[Α\], περιόδου \[Τ\] και μήκους κύματος \[λ\]. Στο παρακάτω σχήμα φαίνεται η μεταβολή του πλάτους σημείου Σ της επιφάνειας του υγρού με το χρόνο. Ποιες από τις παρακάτω προτάσεις είναι σωστές;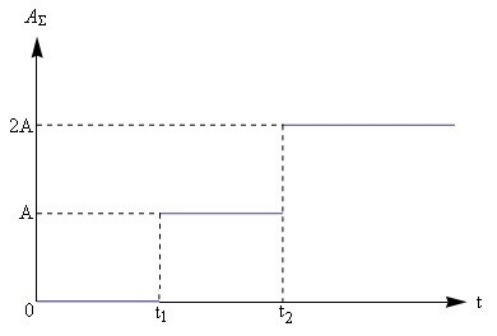
15. Σε ομογενή χορδή που ταυτίζεται με τον ημιάξονα \[Ox\] διαδίδεται εγκάρσιο αρμονικό κύμα που περιγράφεται απ’ τη σχέση \[y=A ημ2π\left( \frac{t}{T}-\frac{x}{λ} \right) \]. Στο παρακάτω διάγραμμα φαίνεται η μεταβολή της φάσης των σημείων του μέσου τη στιγμή \[t_1\]. Ποιες από τις παρακάτω προτάσεις είναι σωστές;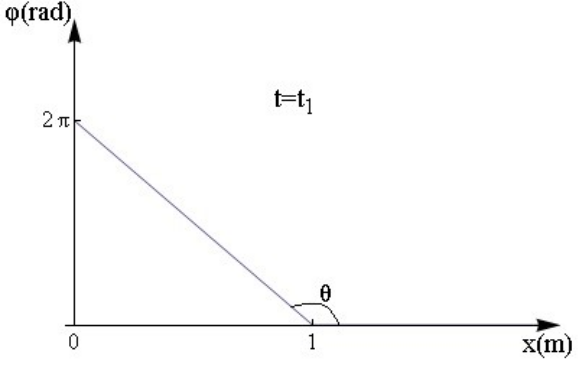
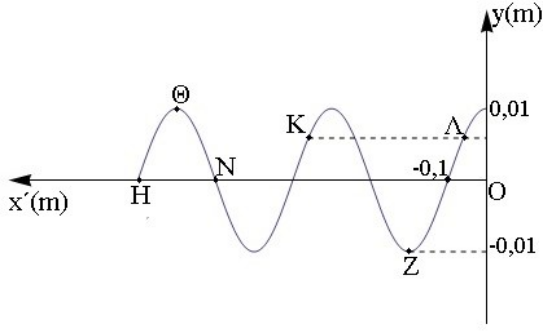
20. Δύο σύγχρονες πηγές κυμάτων \[Π_1\, ,\, Π_2\] δημιουργούν στην επιφάνεια υγρού εγκάρσια αρμονικά κύματα ίδιου πλάτους \[Α\] και περιόδου \[Τ\]. Σημείο Ζ της επιφάνειας απέχει απ’ τις δύο πηγές αποστάσεις \[r_1=2\, m\] και \[r_2=1,75\, m\]. Η ταχύτητα διάδοσης του κύματος είναι \[υ_δ=2\, \frac{m}{s}\]. Για να παραμένει το Ζ συνεχώς ακίνητο μετά τη συμβολή τότε η συχνότητα των δύο πηγών πρέπει να παίρνει τις τιμές: 23. Αρμονικό κύμα διαδίδεται κατά τη διεύθυνση του άξονα \[x' Ox\]. Η εξίσωση του κύματος δίνεται απ’ τη σχέση \[y=A ημ2π\left(\frac{t}{T}-\frac{x}{λ}\right)\]. Στο παρακάτω διάγραμμα φαίνεται το στιγμιότυπο του κύματος τη χρονική στιγμή \[t_1\]. Ποιες από τις παρακάτω προτάσεις είναι σωστές;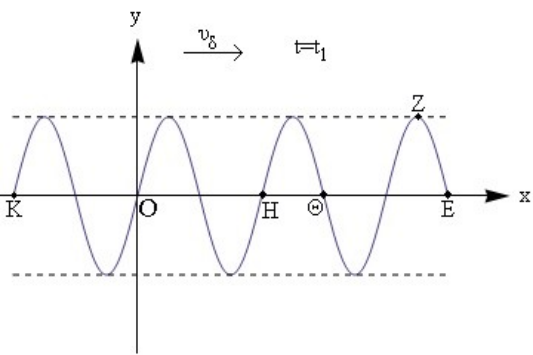
25. Κατά μήκος οριζόντιου ελαστικού μέσου που ταυτίζεται με τη διεύθυνση του άξονα \[x' x\] διαδίδεται εγκάρσιο αρμονικό κύμα που περιγράφεται απ’ την εξίσωση \[y=0,1 ημ \frac{π}{2} (t-8x)\] (S.I.). Ποιες από τις παρακάτω προτάσεις είναι σωστές; 27. Σε οριζόντια ελαστική χορδή που ταυτίζεται με τον άξονα \[x' Ox\] διαδίδεται εγκάρσιο αρμονικό κύμα. Σημείο Κ που βρίσκεται στη θέση \[x_K=-1,5\, m\] έχει τη χρονική στιγμή \[t_1\] φάση \[φ_{Κ,1}=6π\, rad\] ενώ σημείο Λ που βρίσκεται στη θέση \[x_Λ=1,5\, m\] έχει τη χρονική στιγμή \[t_2=t_1-\frac{3T}{2}\] και φάση \[φ_{Λ,2}=5π\, rad\]. 29. Εγκάρσιο αρμονικό κύμα διαδίδεται κατά τη διεύθυνση του άξονα \[x' x\] σε γραμμικό ελαστικό μέσο. Η εξίσωση της ταχύτητας των σημείων του μέσου είναι \[υ=0,02π\, συνπ(2t+x)\] (S.I.). Ποιες από τις παρακάτω προτάσεις είναι σωστές; 30. Στο παρακάτω σχήμα φαίνεται το στιγμιότυπο τη στιγμή \[t_1\] εγκάρσιου αρμονικού κύματος που διαδίδεται κατά την αρνητική φορά στον άξονα \[Ox'\]. Η αρχή του άξονα Ο αρχίζει να ταλαντώνεται την \[t=0\] με θετική ταχύτητα. Ποιες από τις παρακάτω προτάσεις είναι σωστές;